高中文科数学双曲线总结(高中数学双曲线知识点)
1.高中数学双曲线知识点
去百度文库,查看完整内容>
内容来自用户:鍠冨杻涓濊
双曲线知识点
指导教师:郑军
一、双曲线的定义:
1.第一定义:
到两个定点F1与F2的距离之差的绝对值等于定长(要注意两点:(1)距离之差的绝对值.(2)2a当|MF1|-|MF2|=2a时,曲线仅表示焦点F2所对应的一支;
当|MF1|-|MF2|=-2a时,曲线仅表示焦点F1所对应的一支;
当2a=|F1F2|时,轨迹是一直线上以F1、F2为端点向外的两条射线;
当2a>|F1F2|时,动点轨迹不存在.
2.第二定义:
动点到一定点F的距离与它到一条定直线l的距离之比是常数e(e>1)时,这个动点的轨迹是双曲线这定点叫做双曲线的焦点,定直线l叫做双曲线的准线
二、双曲线的标准方程:
(a>0,b>0)(焦点在x轴上);
(a>0,b>0)(焦点在y轴上);
1.如果项的系数是正数,则焦点在x轴上;如果项的系数是正数,则焦点在y轴上. a不一定大于b.
2.与双曲线共焦点的双曲线系方程是
3.双曲线方程也可设为:例题:已知双曲线和椭圆有相同的焦点,且过点,求双曲线的轨迹方程。
三、点与双曲线的位置关系,直线与双曲线的位置关系:
1点与双曲线:
点在双曲线的内部
点在双曲线的外部
点在双曲线上
2直线与双曲线:(代数法)
设直线,双曲线七、8.29.
2.高中数学双曲线知识点
去百度文库,查看完整内容>内容来自用户:鍠冨杻涓濊双曲线知识点指导教师:郑军一、双曲线的定义:1.第一定义:到两个定点F1与F2的距离之差的绝对值等于定长(要注意两点:(1)距离之差的绝对值.(2)2a当|MF1|-|MF2|=2a时,曲线仅表示焦点F2所对应的一支;当|MF1|-|MF2|=-2a时,曲线仅表示焦点F1所对应的一支;当2a=|F1F2|时,轨迹是一直线上以F1、F2为端点向外的两条射线;当2a>|F1F2|时,动点轨迹不存在.2.第二定义:动点到一定点F的距离与它到一条定直线l的距离之比是常数e(e>1)时,这个动点的轨迹是双曲线这定点叫做双曲线的焦点,定直线l叫做双曲线的准线二、双曲线的标准方程:(a>0,b>0)(焦点在x轴上);(a>0,b>0)(焦点在y轴上);1.如果项的系数是正数,则焦点在x轴上;如果项的系数是正数,则焦点在y轴上. a不一定大于b.2.与双曲线共焦点的双曲线系方程是3.双曲线方程也可设为:例题:已知双曲线和椭圆有相同的焦点,且过点,求双曲线的轨迹方程。
三、点与双曲线的位置关系,直线与双曲线的位置关系:1点与双曲线:点在双曲线的内部点在双曲线的外部点在双曲线上2直线与双曲线:(代数法)设直线,双曲线七、8.29。.。
3.双曲线方程知识点详细总结
去百度文库,查看完整内容>
内容来自用户:linazhang09
双曲线方程1.双曲线的第一定义:
⑴①双曲线标准方程:.
一般方程:.
⑵①i.焦点在x轴上:
顶点: 焦点: 准线方程 渐近线方程:或
ii.焦点在轴上:顶点:. 焦点:.准线方程:. 渐近线方程:或,参数方程:或 .
②轴为对称轴,实轴长为2a,虚轴长为2b,焦距2c. ③离心率. ④准线距(两准线的距离);通径. ⑤参数关系. ⑥焦点半径公式:对于双曲线方程(分别为双曲线的左、右焦点或分别为双曲线的上下焦点)
“长加短减”原则:
构成满足 (与椭圆焦半径不同,椭圆焦半径要带符号计算,而双曲线不带符号)
⑶等轴双曲线:双曲线称为等轴双曲线,其渐近线方程为,离心率.
⑷共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线,叫做已知双曲线的共轭双曲线.与互为共轭双曲线,它们具有共同的渐近线:.
⑸共渐近线的双曲线系方程:的渐近线方程为如果双曲线的渐近线为时,它的双曲线方程可设为.
例如:若双曲线一条渐近线为且过,求双曲线的方程?
解:令双曲线的方程为:,代入得.
⑹直线与双曲线的位置关系:
区域①:无切线,2条与渐近线平行的直线,合计2条;
区域②:即定点在双曲线上,1条切线,2条与渐近线平行的直线,合计3条;
4.高二数学椭圆,抛物线,双曲线整理和总结
圆锥曲线知识点全面覆盖练习1.(1)已知两个定点 , ,且 =10,则点 的轨迹方程是 .(2) 已知两个定点 , ,且 =8, 则点 的轨迹方程是 .(3) 已知两个定点 , ,且 =6, 则点 的轨迹方程是 .2.两焦点分别为 , ,且经过点 的椭圆方程是 .3.若椭圆 上一点P到焦点 的距离等于6,则点P到另一个焦点 的距离是 4. ABC的两个顶点A,B的坐标分别是 , ,边AC,BC所在直线的斜率之积等于 ,则顶点C的轨迹方程是 .5.点P是椭圆 上一点,以点P以及焦点 , 为顶点的三角形的面积等于1, 则点P的坐标是 .6.椭圆 的长轴与半短轴的和等于 , 离心率等于 , 焦点的坐标是 ,顶点的坐标是 ,准线方程是 ,左焦点到右准线的距离等于 .7.椭圆 上一点P到左焦点的距离等于3,则点P到左准线的距离是 ,则点P到右准线的距离是 .8.(1) 已知两个定点 , ,动点P到 的距离的差的绝对值等于6,则点P的轨迹方程是 ;(2) 已知两个定点 , ,动点P到 的距离的差的绝对值等于8, 则点P的轨迹方程是 ;(3) 已知两个定点 , ,动点P到 的距离的差的绝对值等于10, 则点P的轨迹方程是 ;9已知曲线C的方程是 , (1)若曲线C是圆,则 的取值范围是 ; (2)若曲线C是椭圆, 则 的取值范围是 ; (3)若曲线C是双曲线, 则 的取值范围是 .10椭圆 与双曲线 有相同的焦点,则 的取值范围是 .11 ABC的两个顶点A,B的坐标分别是 , ,边AC,BC所在直线的斜率之积等于 ,则顶点C的轨迹方程是 .12双曲线 的实轴长与虚半轴长的和等于 , 离心率等于 , 焦点的坐标是 ,顶点的坐标是 , 准线方程是 ,渐近线的方程 ,两渐近线的夹角等于 ,右支上一点P到左焦点的距离等于10,则它到右准线的距离等于 . 点P到两渐近线的距离的和等于 .13与椭圆 有相同的焦点,且离心率为 的双曲线的方程是 .14点M与点F 的距离比它到直线: 的距离小1,则点 的轨迹方程是 .15抛物线 的焦点的坐标是 , 准线方程是 .16设直线 经过抛物线 的焦点,与抛物线相交于A ,B 两点, (1) = ;(2) = ;(3)若直线 的斜率为1,则 = ; (4) = .17抛物线 上与焦点的距离等于9的点的坐标是 .18正 OAB的三个顶点均在抛物线 上,O为原点,则 OAB的面积等于 .19方程 的两个根可分别作为( )A,一椭圆和一双曲线的离心率 B,两抛物线的离心率C,一椭圆和一抛物线离心率 D,两椭圆的离心率20设 椭圆 的两个焦点,点P在椭圆上,且 . (1) 的面积等于 , (2) 点P的坐标是 .21直线 与椭圆 相交于A,B两点,则 = .22已双曲线的离心率为2,则它的两条渐近线所成的锐角等于 .23如果直线 与双曲线 没有公共点,则 的取值范围是 .24过抛物线 的焦点F的直线与抛物线相交于A,B两点,自A,B向准线作垂线, 垂足分别为 ,则 = .25一动圆与圆 外切,同时与圆 内切,求动圆圆心的轨迹方程.。
5.谁能帮我总结一下数学的椭圆与双曲线的知识点
1.椭圆的几何性质 根据曲线的方程研究曲线的几何性质,并正确地画出它的图形,是解析几何的基本问题之一.根据曲线的条件列出方程.如果说是解析几何的手段,那么根据曲线的方程研究曲线的性质、画图、就可以说是解析几何的目的. 下面我们根据椭圆的标准方程 来研究椭圆的几何性质. (1)范围 引导学生从标准方程 ,得出不等式 , ,即 , .这说明椭圆的直线 和直线 所围成的矩形里(如图),注意结合图形讲解,并指出描点画图时,就不能取范围以外的点. (2)对称性 先让学生阅读教材中椭圆的几何性质2. 设问:为什么“把 换成 ,或把 换 ,或把 、同时换成 、时,方程解不变.则图形关于 轴、轴或原点对称”呢? 事实上,在曲线方程里,如果把 换成 ,而方程不变,那么当点 在曲线上时,点 关于 轴的对称点 也在曲线上,所以曲线关于 轴对称.类似地可以证明其他两个命题. 同时应向学生指出:如果曲线具有关于 轴对称,关于 轴对称和关于原点对称中的任意两种,那么它一定具有另一种对称. 最后强调: 轴、轴是椭圆的对称轴.原点是椭圆的对称中心即椭圆中心.进而说明椭圆的中心是焦点连线的中点,对称轴是焦点的连线及其中垂线与坐标系无关.因而是曲线的固有性质. (3)顶点 引导学生从椭圆的标准方程 分析它与 轴、轴的交点,只须令 得 ,点 、是椭圆与 轴的两个交点;令 得 ,点 、是椭圆与 轴的两个交点.应该强调:椭圆有四个顶点 、、、. 同时还需指出: (1°)线段 和 分别叫做椭圆的长轴和短轴,它们的长分别等于 和 ; (2°) 、的几何意义: 是椭圆长半轴的长, 是椭圆短半轴的长. (3°)椭圆的顶点即是椭圆与对称轴的交点,一般二次曲线的顶点即是曲线与其对称轴的交点. 这时教师可作如下小结:由椭圆的范围,对称性和顶点,再进行描点画图,只须描出较少的点,就可以得到较正确的图形. (4)离心率 由于离心率的概念比较抽象,教师可直接给出离心率的定义: 椭圆的焦距与长轴长的比 ,叫做椭圆的离心率. 先分析离心率 的取值范围: ∵ , ∴ . 再结合图表分析离心率的大小对椭圆形状的影响: (1)当 趋近于1时, 趋近于 ,从而 越小,因此椭圆越扁平: (2)当 趋近于0时, 趋近于0,从而 趋近于 ,因此椭圆越接近于圆.2..文字语言定义 平面内一个动点到一个定点与一条定直线的距离之比是一个大于1的常数。
定点是双曲线的焦点,定直线是双曲线的准线,常数e是双曲线的离心率。2.集合语言定义 设 双曲线上有一动点M,定点F,点M到定直线距离为d, 这时称集合{M| |MF|/d=e,e>1}表示的点集是双曲线. 注意:定点F要在定直线外 且 比值大于1. 3.标准方程 设 动点M(x,y),定点F(c,0),点M到定直线l:x=a^2/c的距离为d, 则由 |MF|/d=e>1. 推导出的双曲线的标准方程为 (x²/a²)-(y²/b²)=1 其中a>0,b>0,c²=a²+b². 这是中心在原点,焦点在x轴上的双曲线标准方程. 而中心在原点,焦点在y轴上的双曲线标准方程为: (y²/a²)-(x²/b²)=1. 同样的:其中a>0,b>0,c²=a²+b².编辑本段·双曲线的简单几何性质 1、轨迹上一点的取值范围:x≥a,x≤-a(焦点在x轴上)或者y≥a,y≤-a(焦点在y轴上)。
2、对称性:关于坐标轴和原点对称。 3、顶点:A(-a,0), A'(a,0)。
同时 AA'叫做双曲线的实轴且∣AA'│=2a. B(0,-b), B'(0,b)。同时 BB'叫做双曲线的虚轴且│BB'│=2b. 4、渐近线: 焦点在x轴:y=±(b/a)x. 焦点在y轴:y=±(a/b)x. 圆锥曲线ρ=ep/1-ecosθ当e>1时,表示双曲线。
其中p为焦点到准线距离,θ为弦与X轴夹角 令1-ecosθ=0可以求出θ,这个就是渐近线的倾角。θ=arccos(1/e) 令θ=0,得出ρ=ep/1-e, x=ρcosθ=ep/1-e 令θ=PI,得出ρ=ep/1+e ,x=ρcosθ=-ep/1+e 这两个x是双曲线定点的横坐标。
求出他们的中点的横坐标(双曲线中心横坐标) x=【(ep/1-e)+(-ep/1+e)】/2 (注意化简一下) 直线ρcosθ=【(ep/1-e)+(-ep/1+e)】/2 是双曲线一条对称轴,注意是不与曲线相交的对称轴。 将这条直线顺时针旋转PI/2-arccos(1/e)角度后就得到渐近线方程,设旋转后的角度是θ' 则θ'=θ-【PI/2-arccos(1/e)】 则θ=θ'+【PI/2-arccos(1/e)】 带入上式: ρcos{θ'+【PI/2-arccos(1/e)】}=【(ep/1-e)+(-ep/1+e)】/2 即:ρsin【arccos(1/e)-θ'】=【(ep/1-e)+(-ep/1+e)】/2 现在可以用θ取代式中的θ'了 得到方程:ρsin【arccos(1/e)-θ】=【(ep/1-e)+(-ep/1+e)】/2 5、离心率: 第一定义: e=c/a 且e∈(1,+∞). 第二定义:双曲线上的一点P到定点F的距离│PF│ 与 点P到定直线(相应准线)的距离d 的比等于双曲线的离心率e. d点(│PF│)/d线(点P到定直线(相应准线)的距离)=e 6、双曲线焦半径公式(圆锥曲线上任意一点P(x,y)到焦点距离) 右焦半径:r=│ex-a│ 左焦半径:r=│ex+a│ 7、等轴双曲线 一双曲线的实轴与虚轴长相等 即:2a=2b 且 e=√2 这时渐近线方程为:y=±x(无论焦点在x轴还是y轴) 8、共轭双曲线 双曲线S'的实轴是双曲线S的虚轴 且 双曲线S'的虚轴是双曲线S的实轴时,称双曲线S'与双曲线S为共轭双曲线。
几何表达:S:(x^2/a^2)-(y^2/b^2)=1 S':(y^2/b^2)-(x^2/a^2)=1 特点:(1)共渐近线 (2)焦距相等 (3)两双曲线的离心率平方后。
6.哪位大事能给我归纳一下高中数学解析几何啊,椭圆,双曲线,抛物线
(一)椭圆及其标准方程 1. 椭圆的定义:椭圆的定义中,平面内动点与两定点F1、F2的距离的和大于|F1F2|这个条件不可忽视.若这个距离之和小于| F1F2|,则这样的点不存在;若距离之和等于 | F1F2|,则动点的轨迹是线段F1F2 2.椭圆的标准方程:x²/a²+y²/b²=1(a>b>0),y²/a²+x²/b²=1(a>b>0). 3.椭圆的标准方程判别方法:判别焦点在哪个轴只要看分母的大小:如果x²项的分母大于y²项的分母,则椭圆的焦点在x轴上,反之,焦点在y轴上. 4.求椭圆的标准方程的方法:⑴ 正确判断焦点的位置;⑵ 设出标准方程后,运用待定系数法求解. (二)椭圆的简单几何性质 1. 椭圆的几何性质:设椭圆方程为x²/a²+y²/b²=1(a>b>0). ⑴ 范围: -a≤x≤a,-b≤x≤b,所以椭圆位于直线x=±a和y=±b所围成的矩形里. ⑵ 对称性:分别关于x轴、y轴成轴对称,关于原点中心对称.椭圆的对称中心叫做椭圆的中心. ⑶ 顶点:有四个A1(-a,0)、A2(a,0)B1(0,-b)、B2(0,b). 线段A1A2,B1B2分别叫做椭圆的长轴和短轴.它们的长分别等于2a和2b,a和b分别叫做椭圆的长半轴长和短半轴长. 所以椭圆和它的对称轴有四个交点,称为椭圆的顶点. ⑷ 离心率:椭圆的焦距与长轴长的比e=c/a叫做椭圆的离心率.它的值表示椭圆的扁平程度.0b>0)的准线有两条,它们的方程为x=±(a²/c).对于椭圆y²/a²+x²/b²=1(a>b>0)的准线方程,只要把x换成y就可以了,即y= ±(a²/c). 3.椭圆的焦半径:由椭圆上任意一点与其焦点所连的线段叫做这点的焦半径. 设F1(-c,0),F2(c,0)分别为椭圆x²/a²+y²/b²=1(a>b>0)的左、右两焦点,M(x,y)是椭圆上任一点,则两条焦半径长分别为|MF1|=a+ex,|MF2|=a+ex. 椭圆中涉及焦半径时运用焦半径知识解题往往比较简便. 椭圆的四个主要元素a、b、c、e中有a²=b²+c²,e=c/a两个关系,因此确定椭圆的标准方程只需两个独立条件. 4.椭圆的参数方程 椭圆x²/a²+y²/b²=1(a>b>0)的参数方程为x=acosθ,y=bsinθ(θ为参数). 说明:⑴ 这里参数θ叫做椭圆的离心角.椭圆上点P的离心角θ与直线OP的倾斜角α不同:tanα=(b/a)tanθ; ⑵ 椭圆的参数方程可以由方程x²/a²+y²/b²=1与三角恒等式sin²θ+cos²θ=1相比较而得到,所以椭圆的参数方程的实质是三角代换. 5.椭圆的的内外部 (1)点P(x0,y0)在椭圆x²/a²+y²/b²=1(a>b>0)的内部,得出x0²/a²+y0²/b²b>0)的外部,得出 x0²/a²+y0²/b²>1. 6. 椭圆的切线方程 (1)椭圆x²/a²+y²/b²=1(a>b>0)上一点P(x0,y0)处的切线方程是(x0•x)/a²+(y0•y)/b²=1. (2)过椭圆x²/a²+y²/b²=1(a>b>0)外一点P(x0,y0)所引两条切线的切点弦方程是(x0•x)/a²+(y0•y)/b²=1. (3)椭圆x²/a²+y²/b²=1(a>b>0)与直线Ax+By+C=0相切的条件是A²a²+B²b²=c² (三)双曲线及其标准方程 1.双曲线的定义:平面内与两个定点 、的距离的差的绝对值等于常数2a(小于|F1F2|)的动点M的轨迹叫做双曲线.在这个定义中,要注意条件2a|F1F2|,则无轨迹.若|MF1||MF2|时,轨迹为 双曲线的另一支.而双曲线是由两个分支组成的,故在定义中应为“差的绝对值”. 2.双曲线的标准方程:x²/a²-y²/b²=1和y²/a²+x²/b²=1(a>0,b>0).这里b²=c²-a²,其中|F1F2|=2c.要注意这里的a、b、c及它们之间的关系与椭圆中的异同. 3.双曲线的标准方程判别方法是:如果x²项的系数是正数,则焦点在x轴上;如果 项的系数是正数,则焦点在y轴上.对于双曲线,a不一定大于b,因此不能像椭圆那样,通过比较分母的大 小来判断焦点在哪一条坐标轴上. 4.求双曲线的标准方程,应注意两个问题:⑴ 正确判断焦点的位置;⑵ 设出标准方程后,运用待定系数法求解. (四)双曲线的简单几何性质 1.双曲线:x²/a²-y²/b²=1的实轴长为2a,虚轴长为2b,离心率e=c/a>1,离心率e越大,双曲线的开口越大. 2. 双曲线:x²/a²-y²/b²=1的渐近线方程为y=±(b/a)或表示为:x²/a²-y²/b²=0.若已知双曲线的渐近线方程是y=±(m/n)x,即mx±ny=0,那么双曲线的方程具有以下形式:m²x²- n²y²=k,其中k是一个不为零的常数. 3.双曲线的第二定义:平面内到定点(焦点)与到定直线(准线)距离的比是一个大于1的常数(离心率)的点的轨迹叫做双曲线.对于双曲线:x²/a²-y²/b²=1,它的焦点坐标是(-c,0) 和(c,0),与它们对应的准线方程分别是x=-a²/c和x=a²/c.双曲线:x²/a²-y²/b²=1(a>0,b>0)的焦半径公式|PF1|=|e(x+a²/c)|,|PF2|=|e(-x+a²/c)|. 4.双曲线的内外部 (1)点P(x0,y0)在双曲线x²/a²-y²/b²=1(a>0,b>0)的内部,得出x0²/a²-y0²/b²0,b>0)的外部,得出x0²/a²-y0²/b²>1. 5.双曲线的方程与渐近线方程的关系 (1)若双曲线方程为x²/a²-y²/b²=1得出渐近线方程:x²/a²±y²/b²=0得出y=±(a/b)x. (2)若渐近线方程为y=±(a/b)x,得出 x²/a²±y²/b²=0,双曲线可设为x²/a²-y²/b²=λ. (3)若双曲线与x²/a²-y²/b²=1有公共渐近线,可设为x²/a²-y²/b²=λ(λ>0,焦点在x轴上,λ0,b>0)上一点P(x0,y0)处的切线方程是(x0•x)/a²-(y0•y)/b²=1. (2)过双曲线x²/a²-y²/b²=1(a>0,b>0)外一点P(x0,y0)所引两条切。
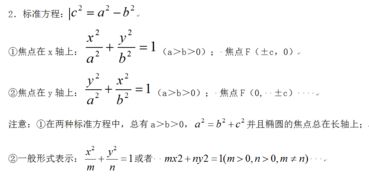
相关推荐
声明:本网站尊重并保护知识产权,根据《信息网络传播权保护条例》,如果我们转载的作品侵犯了您的权利,请在一个月内通知我们,我们会及时删除。
蜀ICP备2020033479号-4 Copyright © 2016 学习鸟. 页面生成时间:3.896秒









