数独的知识基础(数独有什么知识)

1.数独有什么知识

1.联除法. 在并排的三个九宫格中的两排寻找相同数字，再利用九宫格得出另一排中该数字位置，该方法适用于中高级数独. 2.巡格法 找出在每个九宫格中出现频率较高的数字，得出该数字在其余九宫格内位置，该方法应用于方法一之后. 3.排它法 这个方法是解决问题的关键，易被常人所忽略.在各行列或九宫格中观察，若有个位置其它数字都不能填，就填余下的数字 4.待定法 此方法不常用却很有效.暂时确定某个数字在某个区域，再利用其来进行排除 5.行列法 此方法用于收官阶段，利用先从行列突破来提高解题效率. 6.假设法 作为一名高手，我不提倡这种方法.即在某个位置随机的填上一个数字，再进行推演，并有可能最终产生矛盾而否定结论. 7.频率法 这种方法相比于上一种方法更能提高效率.在某一行列或九宫格列举出所有情况，再选择某位置中出现频率高的数字。

2.紧急

【转摘】

“数独”（日语是すうどく，英文为Sudoku）

“数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。概括来说，它就是一种填数字游戏。但这一概念最初并非来自日本，而是源自拉丁方块，它是十八世纪的瑞士数学家欧拉发明的。出生于1707年的欧拉被誉为有史以来最伟大的数学家之一。

欧拉从小就是一个数学天才，大学时他在神学院里攻读古希伯来文，但却连续13次获得巴黎科学院的科学竞赛的大奖。

1783年，欧拉发明了一个“拉丁方块”，他将其称为“一种新式魔方”，这就是数独游戏的雏形。不过，当时欧拉的发明并没有受到人们的重视。直到20世纪70年代，美国杂志才以“数字拼图”的名称将它重新推出。

1984年日本益智杂志Nikoli的员工金元信彦偶然看到了美国杂志上的这一游戏，认为可以用来吸引日本读者，于是将其加以改良，并增加了难度，还为它取了新名字称做“数独”，结果推出后一炮而红，让出版商狂赚了一把。至今为止，该出版社已经推出了21本关于数独的书籍，有一些上市后很快就出现了脱销。

数独后来的迅速走红，主要归功于一位名叫韦恩·古尔德的退休法官。古尔德现在居住在爱尔兰，1997年，无意中发现这个游戏，并编写了一个计算机程序来自动生成完整的数独方阵。2004年年底，伦敦《时报》在古尔德的建议下开辟了数独专栏，《每日电讯报》紧随其后，在2005年1月登出了数独。后来，世界各国数十家日报相继开辟专栏来介绍数独，有的甚至把它摆在头版大肆炒作，招揽读者。专门介绍这种娱乐的杂志和一本又一本的书籍如雨后春笋般涌现，相关的比赛，网站和博客等等，也接二连三地冒出来。

此外，出版商还授权软件商开发了上百个数独游戏软件。供人们在网上购买。目前，日本共有5家数独月刊，总发行量为66万份。由于数独在日本已经被注册商标，其他竞争者只好使用其最初在美国的名字“数字拼图”。

数独游戏和传统的填字游戏类似，但因为只使用1到9的数字，能够跨越文字与文化疆域，所以被誉为是全球化时代的魔术方块。

数独游戏进入英国后，很多人立刻迷上了它。由于该游戏简单易学，而且初级游戏并不难，所以很多人在工作休息时间以及乘车上班途中都是埋头在报纸上狂玩数独。更有人宣称多玩数独游戏可以延缓大脑衰老。

目前，英国涌现出了大量的关于数独游戏的书籍，专门推广此类游戏的网站也纷纷出现，人们可以从网上下载数独软件到电脑，也可以把软件下载到手机上玩。

规则简单易掌握

数独的游戏规则很简单，9x9个格子里，已有若干数字，其它宫位留白，玩家需要自己按照逻辑推敲出剩下的空格里是什么数字，使得每一行与每一列都有1到9的数字，每个小九宫格里也有1到9的数字，并且一个数字在每个行列及每个小九宫格里都只能出现一次。

做这种游戏不需要填字谜那样的语言技巧和文化知识，甚至也不需要复杂的数学能力。因为它根本不需要加减乘除运算。当然，你也千万别小看它，并不是那么容易被“制服”的。当你握笔沉思的时候，这9个数字很可能让你头痛不已，脉搏加快，恼火不已。不过，当你成功填完所有数字的时候，你肯定会感到欣喜若狂。有数独迷宣称，做此类游戏，一名大学教授很可能不敌一名工厂工人。

看起来很像中国古代的九宫格。

3.数独游戏初学者怎么玩

数独游戏初学者可以使用数独的基础解法，基础解法包括排除法（摒除法）和唯一余数法。用数字去找单元内唯一可填空格，称为摒除法，数字可填唯一空格称为摒余解（Hidden Single）。用格位去找唯一可填数字，称为余数法，格位唯一可填数字称为唯余解（Naked Single）。

一、排除法（摒除法）

摒除，利用数字在同一行、列、宫内不得重复的情况，进而进行排除的一种逻辑，也叫排除。

1、数字可填唯一空格在「宫」单元称为宫排除（Hidden Single in Box），也称宫摒除法。

2、数字可填唯一空格在「行」单元称为行排除法（Hidden Single in Row），也称行摒除法。

3、数字可填唯一空格在「列」单元称为列排除法（Hidden Single in Column），也称列摒除法。

二、唯一余数法

解九宫格的一种方法，余数法的观点是点算某格的等位群格位中已经出现过哪些数，如果已经出现1 – 9中的8格，那么这格就是第9个数，此数被称为唯一余数。余数法是删减等位群格位（Peer）已出现的数字的方法，每一格位的等位群格位有20个。

扩展资料

数独进阶解法包括：区块摒除法（Locked Candidates）、数组（Subset/Tuple）、二链列（X-Wing）、唯一矩形（Unique Rectangle）、全双值格致死解法（Bivalue Universal Grave）、同数链（X-Chain）、异数链（Multidigit Chain）及其他数链的高级技巧等等。

通过基础解法出数只需一种解法，摒除法或唯余法，超出此范围而需要施加进阶解法时，解题点需要进阶解法协助基础解法来满足隐性唯一或显性唯一才能出数，该解题点的解法需要多个步骤协力完成，因此称做组合解法。

参考资料来源：搜狗百科--数独

参考资料来源：搜狗百科--唯一余数法

4.正确数独规则

数独顾名思义——每个数字只能出现一次.数独盘面是个九宫，每一宫又分为九个小格.在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字.使1-9每个数字在每一行、每一列和每一宫中都只出现一次.这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式.

数独解法全是由规则衍生出来的，基本解法分为两类思路，一类为排除法，一类为唯一法.更复杂的解法，最终也会归结到这两大类中.数独直观法解题技巧主要有：唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法，余数测试法等.

5.数独技巧的方法技巧

数独解法全是由规则衍生出来的。

基本解法分为两类思路，一类为排除法，一类为唯一法。更复杂的解法，最终也会归结到这两大类中。

下边以图示简单介绍几种解法，只要你花几分钟看一遍，马上就可以开始做数独了。数独直观法解题技巧主要有：唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法、余数测试法等。

基础摒除法就是利用1~9的数字在每一行、每一列、每一个九宫格都只能出现一次的规则进行解题的方法。基础摒除法可以分为行摒除、列摒除、九宫格摒除。

实际寻找解的过程为：寻找九宫格摒除解：找到了某数在某一个九宫格可填入的位置只余一个的情形；意即找到了该数在该九宫格中的填入位置。寻找列摒除解：找到了某数在某列可填入的位置只余一个的情形；意即找到了该数在该列中的填入位置。

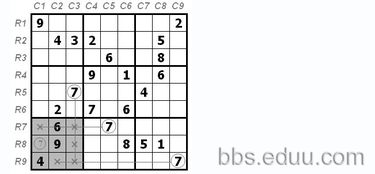
看能用基础摒除法确定B2、C8、E7、F6、I5的数字吗？A4=9，则A行其它格排除9,G1=9，第1列排除数字9,D3=9，第3列排除数字9。由基础摒除法，第A1所在的九宫格内9只有1个位置，即B2。

A4=9，则4列其它格排除9,G1=9，第G行排除数字9,H9=9，第H行排除数字9。由基础摒除法，第G4所在的九宫格内9只有一个唯一的位置，即确定I5=9。

A4=9，则4列其它格排除9,D3=9，第D行排除数字9,I5=9，第5列排除数字9。由基础摒除法，第D4所在的九宫格内9只有一个唯一的位置，即确定F6=9。

A4=9，则A行其它格排除9,B2=9，第B行排除数字9,H9=9，第9列排除数字9。由基础摒除法，第A7所在的九宫格内9只有一个唯一的位置，即确定C8=9。

C8=9，则8列其它格排除9,D3=9，第D行排除数字9,F6=9，第F行排除数字9,H9=9，第9列排除数字9。由基础摒除法，第D7所在的九宫格内9只有一个唯一的位置，即确定E7=9。

唯余解法就是某宫格可以添入的数已经排除了8个，那么这个宫格的数字就只能添入那个没有出现的数字。A5=？，其实这就是唯余解法的原理，很简单，但是实际使用时就不会容易发现了。

能使用唯余解法确定B7的值吗？能确定E9,A9,B9,C9的值吗？由区块摒除法可以得出E9=9。由唯余解法，C9=2。

同样，可以得到其他。 区块摒除法是基础摒除法的提升方法，是直观法中使用频率最高的方法之一。

所谓区块，就是将行分成3个三个相连的小方块构成，列也是分成3个三个相连的小方块构成.九宫格同样被看成由3个三个相连的小方块构成，如下面示意图：区块摒除法的核心思想如下面解释（以行为例），对于在列也是相同的道理。假如（G1~G3）黄色区域区块其中之一是数字9。

则，（H4~H6）蓝色区域可能含有数字9，否则（I4~I6）绿色区域含有数字9。假定我们已确定（G1~G3）黄色区域区块其中之一是数字9,(H4~H6)蓝色区域含有数字9，则：在（I7~I9）绿色区域一定含有数字9.如果再通过其它方法确定（I7~I9）绿色区域中某两个宫格不能为数字9，则就能确定数字9在（I7~I9）区块的具体位置。

当某个小九宫格中有一行已有3个数字时，我们将这2个数所在的行称为“撑”。这时，在该行另外两个小九宫格上的另外两行寻找该小九宫格没有的数字，将该数的位置称为“点”。

那么，“点”上的数字在“撑”所在的九宫格中必然位于“撑”和“点”所在行以外的另一行；同时，“点”上的数字在“撑”和“点”以外的另一九宫格中位于“撑”所在的行上。小九宫格六中F行已经填满数字5、4、1，此时5、4、1就已经就构成“撑”。

而在F行上的小九宫格四和小九宫格五中出现的小九宫格六中不存在的数为E2格中的数字6即为“点”。根据撑点定位法，在小九宫格六中，“点”上的数字6不会出现在E行和F行，所以很快能推断出数字6在小九宫格六中只能出现在D行，即只能出现在D7格。

同时，还可以推断出数字6在小九宫格五中只能出现在“撑”的所在的F行，进而推断出F5格为6。 所谓余数测试法就是在某行或列，九宫格所填数字比较多，剩余2个或3个时，在剩余宫格添入值进行测试的解题方法。

在B行，C行剩余未填的数字只有两三个了，这时可以使用余数测试法进行解题。我们看B行，B3可能添入的数为5或者6，我们从5开始测试我们在B3添入5进行测试，得到左图，没有得出出错的推断，所以B3=5可能是正确的判断，如果能判断出B3不能添6，则才能肯定B3=5。

所以下面我们还需要用B3=6进行测试。在B3添入6，推出A1=5.观察A5,A6，必含数字5，证明B3=6是错误的.从而得出B3=5。

候选数法解题的过程就是逐渐排除不合适的候选数的过程，当某个宫格的候选数排除到只有一个数的时候，那么这个数就是该宫格的唯一的一个候选数，这个候选数就可以解了。隐性唯一候选数法 当某个数字在某一列各宫格的候选数中只出现一次时，那么这个数字就是这一列的唯一候选数了.这个宫格的值就可以确定为该数字.这时因为，按照数独游戏的规则要求每一列都应该包含数字1~9，而其它宫格的候选数都不含有该数，则该数不可能出现在其它的宫格，那么就只能出现在这个宫格了.对于唯一候选数出现行，九宫格的情况，处理方法完全相同。

这是制作好的一张候选数表，注意观察B5,B9,D1。可以看出在第1列，。

6.解开数独的依据和基本步骤是什么

9x9个格子里，已有若干数字，其它宫位留白，你需要自己按照逻辑推敲出剩下的空格里是什么数字，使得每一行与每一列都有1到9的数字，每个小九宫格里也有1到9的数字，并且一个数字在每个行列及每个小九宫格里都只能出现一次。 这种游戏不需要填字谜那样的语言技巧和文化知识，甚至也不需要复杂的数学能力，因为根本不需要你加减乘除来运算。玩数独这类游戏，可以说一名大学教授可能还不如一名工厂工人。

数独同法：首先，第一步：看横行（原则：这行已确定数大于等于四）

每一个空格写入可能的数字（根据横纵行已有的，但不看九宫）

第二步：看九宫

划去无机会的数字

第三步；重复1

第四步：重复2

此时，已基本每个空格都有数字了（一般数独已解），并且横纵行，九宫原则（明显原则）均已用尽.

隐含原则1：{若一个单元（横行\纵行\九宫）某组内未确定格数，与其内部元素数相同，则这几个元素必在这几格内}例：

某一横行内所填确定数字如下：

(1.2)(6)(2.3.4)(7)(5.3)(9)(2.4)(8)(1.4)

在第1.3.7.9格（4个）内含1.2.3.4四个元素

所以，这四个数只能在其中，所以第五格内3去掉

第五步：重复1.2，利用隐含原则1

第六步：检验全局，利用1_5

此时仅仅余下几个格了（难的数独已解），还有第二隐含原则：

(1.2)(6)(2.3.4)(7)(5.3,8)(9,1)(2.4)(8,9)(1.4)

这一行很复杂，隐含原则一也很难奏效

但可见，数5在这一行仅有一次机会，所以，第五格只能是它！

第七步：重复1.2，利用隐含原则2

第八步：检验全局，利用1_7

所有数独已解，若解不出来，三种原因

1你解错了 2有一个条件没看见 3这个数独有问题

完毕！