高中数学三角函数点及答案(高中数学必修四三角函数的重点知识点)

1.高中数学必修四三角函数的重点知识点

两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA) 倍角公式 tan2A = 2tanA/(1-tan^2 A) Sin2A=2SinA•CosA Cos2A = Cos^2 A--Sin^2 A =2Cos^2 A—1 =1—2sin^2 A 三倍角公式 sin3A = 3sinA-4(sinA)^3; cos3A = 4(cosA)^3 -3cosA tan3a = tan a • tan（π/3+a）• tan（π/3-a） 半角公式 sin(A/2) = √{（1--cosA）/2} cos(A/2) = √{（1+cosA）/2} tan(A/2) = √{（1--cosA）/(1+cosA)} cot(A/2) = √{（1+cosA）/(1-cosA)} tan(A/2) = (1--cosA)/sinA=sinA/(1+cosA) 和差化积 sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosB 积化和差 sin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)] 诱导公式 sin(-a) = -sin(a) cos(-a) = cos(a) sin（π/2-a） = cos(a) cos（π/2-a） = sin(a) sin（π/2+a） = cos(a) cos（π/2+a） = -sin(a) sin（π-a） = sin(a) cos（π-a） = -cos(a) sin（π+a） = -sin(a) cos（π+a） = -cos(a) tgA=tanA = sinA/cosA 公式一： 设α为任意角，终边相同的角的同一三角函数的值相等： sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot(2kπ+α)= cotα 公式二： 设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin（π+α）= -sinα cos（π+α）= -cosα tan（π+α）= tanα cot（π+α）= cotα 公式三： 任意角α与 -α的三角函数值之间的关系： sin（-α）= -sinα cos（-α）= cosα tan（-α）= -tanα cot（-α）= -cotα 公式四： 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin（π-α）= sinα cos（π-α）= -cosα tan（π-α）= -tanα cot（π-α）= -cotα 公式五： 利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六： π/2±α及3π/2±α与α的三角函数值之间的关系： sin（π/2+α）= cosα cos（π/2+α）= -sinα tan（π/2+α）= -cotα cot（π/2+α）= -tanα sin（π/2-α）= cosα cos（π/2-α）= sinα tan（π/2-α）= cotα cot（π/2-α）= tanα sin(3π/2+α)= -cosα cos(3π/2+α)= sinα tan(3π/2+α)= -cotα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα （以上k∈Z）。

2.谁能给我提供一份高中数学三角函数基础知识

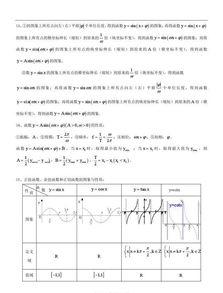
一.三角函数：1、有关角的概念：任意角、象限角、区间角、终边相同的角.2、弧度制： 1弧度定义，弧度制与角度制的互化，扇形面积公式.圆心角 .3、三角函数的定义：正弦、余弦、正切、余切、正割、余割的定义和符号.例1. 角的终边上一点p的坐标为（4t,-3t）(t≠0)，求角的各三角函数值. 分t>0与t<0讨论，略4、三角函数线的定义和作法.5、⑴同角三角函数关系：平方关系、商数关系、倒数关系；⑵诱导公式：kπ±α（k=0,1，）与α的各种三角关系式. 例2：已知：. 例3：设sina+cosa=k，若sin 3a+cos3a<0成立，则k的取值范围为.6、三角函数图象 ⑴函数 作法：变换法、五点法；⑵三角函数性质：定义域、值域、单调性、奇偶性、周期性、最值；⑶三角函数性质运用：①已知一角的某一三角函数值，求该角的其它三角函数值；②化简三角函数式；③证明三角恒等式；④求三角函数定义域、值域：（I）求定义域常用方法：三角函数线法、三角函数图象法： 例4、求函数定义域：. 定义域： （II）求值域常用方法：化不同函数为同一函数，化为复合二次函数，应用三角函数值有界性、应用基本不等式.例5、求下列函数值域： ； . 值域： 值域：例6、若则函数的最小值为.例7、函数的单调递减区间为.二.两角和与差的三角函数7、理解、记忆、应用公式的几个问题：⑴公式中角的任意性，公式系统表中，公式是源，要求掌握其推导过程； ⑵公式中的“和差”“倍”“半”均是相对的； ⑶应用公式的灵活性，不仅会“正用”，也要会“逆用”，不仅会用原形，而且还会用“变形”如：.例8、1; .8、三角函数化简、求值、证明 ⑴熟悉各公式及其变换方式；⑵注意函数式的结构特点；⑶注意角之间的变换.例9求值：.答案：1例10、已知：.答案：例11、.答案：直角三角形例12、化简：.答案：三.反三角函数和简单三角方程1、反三角函数概念：反正弦，反余弦，反正切，反余切函数定义及其图象性质.例13、（1）函数的定义域为，值域为；（2）(3)函数的反函数为；（4）用反三角函数表示x：则.2、简单三角方程：可化为同角同函数的方程；一边为0，一边可因式分解的方程；关于sinx、cosx的齐次方程；asinx+bcosx=c型的方程.注意：解三角方程务必记住通解，同时尽量避免非同解变换，以免产生增根失根情况.例14、解方程：（1）cos4x+2cos2x=1；答案： （2）sin|x|=1 ；答案： （3） .答案： = 3??4 * GB3。

3.谁能给我提供一份高中数学三角函数基础知识

一.三角函数： 1、有关角的概念：任意角、象限角、区间角、终边相同的角. 2、弧度制： 1弧度定义，弧度制与角度制的互化，扇形面积公式. 圆心角. 3、三角函数的定义：正弦、余弦、正切、余切、正割、余割的定义和符号. 例1. 角的终边上一点p的坐标为（4t,-3t）(t≠0)，求角的各三角函数值. 分t>0与t<0讨论，略 4、三角函数线的定义和作法. 5、⑴同角三角函数关系：平方关系、商数关系、倒数关系； ⑵诱导公式：kπ±α（k=0,1，）与α的各种三角关系式. 例2：已知：. 例3：设sina+cosa=k，若sin 3a+cos3a<0成立，则k的取值范围为. 6、三角函数图象 ⑴函数 作法：变换法、五点法； ⑵三角函数性质：定义域、值域、单调性、奇偶性、周期性、最值； ⑶三角函数性质运用：①已知一角的某一三角函数值，求该角的其它三角函数值； ②化简三角函数式；③证明三角恒等式；④求三角函数定义域、值域： （I）求定义域常用方法：三角函数线法、三角函数图象法： 例4、求函数定义域：. 定义域： （II）求值域常用方法：化不同函数为同一函数，化为复合二次函数，应用三角函数 值有界性、应用基本不等式. 例5、求下列函数值域： ； . 值域： 值域： 例6、若则函数的最小值为. 例7、函数的单调递减区间为. 二.两角和与差的三角函数 7、理解、记忆、应用公式的几个问题：⑴公式中角的任意性，公式系统表中，公 式是源，要求掌握其推导过程； ⑵公式中的“和差”“倍”“半”均是相对 的； ⑶应用公式的灵活性，不仅会“正用”，也要会“逆用”，不仅会用原形，而 且还会用“变形”如：. 例8、1; . 8、三角函数化简、求值、证明 ⑴熟悉各公式及其变换方式；⑵注意函数式的结构特点；⑶注意角之间的变换. 例9求值：. 答案：1 例10、已知：. 答案： 例11、. 答案：直角三角形 例12、化简：. 答案： 三.反三角函数和简单三角方程 1、反三角函数概念：反正弦，反余弦，反正切，反余切函数定义及其图象性质. 例13、（1）函数的定义域为，值域为； （2）(3)函数的反函数为； （4）用反三角函数表示x：则. 2、简单三角方程：可化为同角同函数的方程；一边为0，一边可因式分解的方程； 关于sinx、cosx的齐次方程；asinx+bcosx=c型的方程. 注意：解三角方程务必记住通解，同时尽量避免非同解变换，以免产生增根 失根情况. 例14、解方程：（1）cos4x+2cos2x=1；答案： （2）sin|x|=1 ；答案： （3） .答案： = 3､4 * GB3。

4.跪求 高中数学三角函数知识点

三角函数是函数，象限符号坐标注。

函数图象单位圆，周期奇偶增减现。同角关系很重要，化简证明都需要。

正六边形顶点处，从上到下弦切割；中心记上数字1，连结顶点三角形；向下三角平方和，倒数关系是对角，顶点任意一函数，等于后面两根除。诱导公式就是好，负化正后大化小，变成锐角好查表，化简证明少不了。

二的一半整数倍，奇数化余偶不变，将其后者视锐角，符号原来函数判。两角和的余弦值，化为单角好求值，余弦积减正弦积，换角变形众公式。

和差化积须同名，互余角度变名称。计算证明角先行，注意结构函数名，保持基本量不变，繁难向着简易变。

逆反原则作指导，升幂降次和差积。条件等式的证明，方程思想指路明。

万能公式不一般，化为有理式居先。公式顺用和逆用，变形运用加巧用；1加余弦想余弦，1减余弦想正弦，幂升一次角减半，升幂降次它为范；三角函数反函数，实质就是求角度，先求三角函数值，再判角取值范围；利用直角三角形，形象直观好换名，简单三角的方程，化为最简求解集 cos（α+β）=cosα•cosβ-sinα•sinβcos（α-β）=cosα•cosβ+sinα•sinβ sin（α±β）=sinα•cosβ±cosα•sinβ tan（α+β）=（tanα+tanβ）/（1-tanα•tanβ） tan（α-β）=（tanα-tanβ）/（1+tanα•tanβ） •和差化积公式： sinα+sinβ=2sin[（α+β）/2]cos[（α-β）/2] sinα-sinβ=2cos[（α+β）/2]sin[（α-β）/2] cosα+cosβ=2cos[（α+β）/2]cos[（α-β）/2] cosα-cosβ=-2sin[（α+β）/2]sin[（α-β）/2] •积化和差公式： sinα•cosβ=（1/2）[sin（α+β）+sin（α-β）] cosα•sinβ=（1/2）[sin（α+β）-sin（α-β）] cosα•cosβ=（1/2）[cos（α+β）+cos（α-β）] sinα•sinβ=-（1/2）[cos（α+β）-cos（α-β）] •倍角公式： sin(2α)=2sinα•cosα=2/(tanα+cotα) cos(2α)=（cosα）^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2 tan(2α)=2tanα/（1-tan^2α） cot(2α)=（cot^2α-1）/(2cotα) sec(2α)=sec^2α/（1-tan^2α） csc(2α)=1/2*secα•cscα •三倍角公式： sin(3α) = 3sinα-4sin^3α = 4sinα•sin(60°+α)sin(60°-α) cos(3α) = 4cos^3α-3cosα = 4cosα•cos(60°+α)cos(60°-α) tan(3α) = （3tanα-tan^3α）/（1-3tan^2α） = tanαtan（π/3+α）tan（π/3-α） cot(3α)=（cot^3α-3cotα）/（3cot^2α-1） •n倍角公式： sin(nα)=ncos^(n-1)α•sinα-C(n,3)cos^(n-3)α•sin^3α+C(n,5)cos^(n-5)α•sin^5α-… cos(nα)=cos^nα-C(n,2)cos^(n-2)α•sin^2α+C(n,4)cos^(n-4)α•sin^4α-… •半角公式： sin（α/2）=±√（（1-cosα）/2) cos（α/2）=±√（（1+cosα）/2) tan（α/2）=±√（（1-cosα）/（1+cosα））=sinα/（1+cosα）=（1-cosα）/sinα cot（α/2）=±√（（1+cosα）/（1-cosα））=（1+cosα）/sinα=sinα/（1-cosα） sec（α/2）=±√（（2secα/（secα+1）) csc（α/2）=±√（（2secα/（secα-1）） •辅助角公式： Asinα+Bcosα=√（A^2+B^2）sin（α+φ）（tanφ=B/A） Asinα+Bcosα=√（A^2+B^2）cos（α-φ）（tanφ=A/B） •万能公式 sin(a)= (2tan(a/2))/(1+tan^2(a/2)) cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2)) tan(a)= (2tan(a/2))/(1-tan^2(a/2)） •降幂公式 sin^2α=（1-cos(2α)）/2=versin(2α)/2 cos^2α=（1+cos(2α)）/2=covers(2α)/2 tan^2α=（1-cos(2α)）/（1+cos(2α)） •三角和的三角函数： sin（α+β+γ）=sinα•cosβ•cosγ+cosα•sinβ•cosγ+cosα•cosβ•sinγ-sinα•sinβ•sinγ cos（α+β+γ）=cosα•cosβ•cosγ-cosα•sinβ•sinγ-sinα•cosβ•sinγ-sinα•sinβ•cosγ tan（α+β+γ）=（tanα+tanβ+tanγ-tanα•tanβ•tanγ）/（1-tanα•tanβ-tanβ•tanγ-tanγ•tanα） •其它公式 •两角和与差的三角函数cos（α+β）=cosα•cosβ-sinα•sinβ cos（α-β）=cosα•cosβ+sinα•sinβ sin（α±β）=sinα•cosβ±cosα•sinβ tan（α+β）=（tanα+tanβ）/（1-tanα•tanβ） tan（α-β）=（tanα-tanβ）/（1+tanα•tanβ） •和差化积公式： sinα+sinβ=2sin[（α+β）/2]cos[（α-β）/2] sinα-sinβ=2cos[（α+β）/2]sin[（α-β）/2] cosα+cosβ=2cos[（α+β）/2]cos[（α-β）/2] cosα-cosβ=-2sin[（α+β）/2]sin[（α-β）/2] •积化和差公式： sinα•cosβ=（1/2）[sin（α+β）+sin（α-β）] cosα•sinβ=（1/2）[sin（α+β）-sin（α-β）] cosα•cosβ=（1/2）[cos（α+β）+cos（α-β）] sinα•sinβ=-（1/2）[cos（α+β）-cos（α-β）] •倍角公式： sin(2α)=2sinα•cosα=2/(tanα+cotα) cos(2α)=（cosα）^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2 tan(2α)=2tanα/（1-tan^2α） cot(2α)=（cot^2α-1）/(2cotα) sec(2α)=sec^2α/（1-tan^2α） csc(2α)=1/2*secα•cscα •三倍角公式： sin(3α) = 3sinα-4sin^3α = 4sinα•sin(60°+α)sin(60°-α) cos(3α) = 4cos^3α-3cosα = 4cosα•cos(60°+α)cos(60°-α) tan(3α) = （3tanα-tan^3α）/（1-3tan^2α） = tanαtan（π/3+α）tan（π/3-α） cot(3α)=（cot^3α-3cotα）/（3cot^2α-1） •n倍角公式： sin(nα)=ncos^(n-1)α•sinα-C(n,3)cos^(n-3)α•sin^3α+C(n,5)cos^(n-5)α•sin^5α-… cos(nα)=cos^nα-C(n,2)cos^(n-2)α•sin^2α+C(n,4)cos^(n-4)α•sin^4α-… •半角公式： sin（α/2）=±√（（1-cosα）/2) cos（α/2）=±√（（1+cosα）/2) tan（α/2）=±√（（1-cosα）/（1+cosα））=sinα/（1+cosα）=（1-cosα）/sinα cot（α/2）=±√（（1+cosα）/（1-cosα））=（1+cosα）/sinα=sinα/（1-cosα） sec（α/2）=±√（（2secα/（secα+1）) csc（α/2）=±√（（2secα/（secα-1）） •辅助角公式： Asinα+Bcosα=√（A^2+B^2）sin（α+φ）（tanφ=B/A） Asinα+Bcosα=√（A^2+B^2）cos（α-φ）（tanφ=A/B） •万能公式 sin(a)= (2tan(a/2))/(1+tan^2(a/2)) cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2)) tan(a)= (2tan(a/2))/(1-tan^2(a/2)） •降幂公式 sin^2α=（1-cos(2α)）/2=versin(2α)/2 cos^2α=（1+co。