你应该知道的浮点数(计算机浮点数的)

1.计算机浮点数的

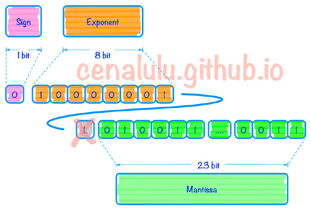
32位浮点数，组成格式是S：符号位，位长1。

0表示正数，1表示负数。M：尾数，位长23，小数点在最前面E：阶符，为了增加表示范围，这里采用移码方式，E=e+127(01111111B) 一个规格化的32位浮点数x的真值可表示为：x=(-1)s*(1.M)*2E-127 e=E-127 1、首先判断符号位S,s=02、要转换2.0,2.0(d) = 10.0000(b) //有关10进制小数转化为2进制的方法，可去网上搜一下。

3、然后将小数转为1.M*2^(E-127)形式10.0000(b) = 1.00000*2^1 = 1.M*2^(E-127) //4、由此M=0H=000000H //(M有效位是24位，2进制的话就是全是0)5、E-127=1 ==> E = 127(d) + 1(d) = 01111111(b) + 00000001(b) = 10000000(b) = 80H 基本过程就是这么算的，题目中2.0换算比较简单，如果换成2.1234，只要在第2步掌握10进制小数转化为2进制的方法就可以了。

2.定点数和浮点数的概念（计算机基础）

浮点数是属于有理数中某特定子集的数的数字表示，在计算机中用以近似表示任意某个实数。

具体的说，这个实数由一个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数次幂得到，这种表示方法类似于基数为10的科学记数法。 浮点计算是指浮点数参与的运算，这种运算通常伴随着因为无法精确表示而进行的近似或舍入。

一个浮点数a由两个数m和e来表示：a = m * be。在任意一个这样的系统中，我们选择一个基数b（记数系统的基）和精度p（即使用多少位来存储）。

m（即尾数）是形如±d.ddd。ddd的p位数（每一位是一个介于0到b-1之间的整数，包括0和b-1）。

如果m的第一位是非0整数，m称作规格化的。有一些描述使用一个单独的符号位（s 代表+或者-）来表示正负，这样m必须是正的。

e是指数。 这种设计可以在某个固定长度的存储空间内表示定点数无法表示的更大范围的数。

例如，一个指数范围为±4的4位十进制浮点数可以用来表示43210,4.321或0.0004321，但是没有足够的精度来表示432.123和43212.3（必须近似为432.1和43210）。当然，实际使用的位数通常远大于4。

此外，浮点数表示法通常还包括一些特别的数值：+∞和−∞（正负无穷大）以及NaN('Not a Number')。无穷大用于数太大而无法表示的时候，NaN则指示非法操作或者无法定义的结果。

大部份计算机采用二进制（b=2）的表示方法。位（bit）是衡量浮点数所需存储空间的单位，通常为32位或64位，分别被叫作单精度和双精度。

有一些计算机提供更大的浮点数，例如英特尔公司的浮点运算单元Intel8087协处理器（以及其被集成进x86处理器中的后代产品）提供80位长的浮点数，用于存储浮点运算的中间结果。还有一些系统提供128位的浮点数（通常用软件实现）。

3.关于浮点数与浮点运算

浮点数实际上就是使用科学记数法来表示数字。

科学记数法就是将一个数字表示为一个1到10之间的小数*10的n次方，比如-3294728可以表示为-3.294728*10^6，这里^代表次方，也就是幂运算。

上面的字母仅仅是个示意，你随便换成谁都可以，只要你自己懂了就行了~

接着说浮点数。计算机里面浮点数就是四个部分：数符——小数的符号，就像我举的例子里面的-号；尾数就是3.294728；阶符就是指数的符号，我举的例子里面因为是正6所以阶符是+；阶码就是幂的数字6。精度决定了你这个数字能精确到多少位，如果精度低那就只有3*10^6，精度高一点3.295*10^6，等等。

关于编程方面的数学，其实和普通的数学差不多，这些底层的东西，如果你不是主业为编程，使用的又是高级一点的语言的话可以暂时不用理解这些东西，编程的时候算法才是灵魂。

如果你主修的是计算机科学得话学校会开课的，如果是业余爱好得话就把高中初中老师教的东西学好就成了