人工智能算法(请问自学AI算法需要懂什么知识?)
1.请问自学AI算法需要懂什么知识?
首先你需要数学基础:高等数学,线性代数,概率论数理统计和随机过程,离散数学,数值分析
其次需要算法的积累:人工神经网络,支持向量机,遗传算法等等算法;当然还有各个领域需要的算法,比如你要让机器人自己在位置环境导航和建图就需要研究SLAM;总之算法很多需要时间的积累;
然后,需要掌握至少一门编程语言,毕竟算法的实现还是要编程的;如果深入到硬件的话,一些电类基础课必不可少;
人工智能一般要到研究生才会去学,本科也就是蜻蜓点水看看而已,毕竟需要的基础课过于庞大。
2.人工智能是什么? 什么是人工智能算法
《博弈圣经》人工智能的定义;人们把理性看成智能、把智能看成(0、1、2、)三维数码、把三维数码看成逻辑,人工智能,也就是理性的三维数码逻辑(+-*÷)精确的运算。
博弈圣经著作人的理论学说;人工智能是什么,人们必须知道什么是思考、什么是思想、什么是智慧?才能对人工智能有一点粗略的认知。
博弈圣经著作人的理论学说;感觉、思维、意识,形成的观念,它会自我构成一致性的思考;它会通过文化的传播方式,以唯心主义的自信、以及对唯物主义认识的思考、在第三空地里产生思想;《博弈圣经》智慧的定义;智慧就是文化进程中独创的执行力。(智能,是理性的三维数码逻辑(+-*÷)的精确运算。
博弈圣经著作人的理论学说;人工智能是数字化三维支点测量,博弈取胜的人工智能,选择一次,都要经过4加、2减、2乘、1除的运算;运算就是对三维支点的运算、三维支点的测量、三维支点的寻找;人工智能是对“天平两端与支点”,也类似于“杠杆两端与支点”对三维空间上的数字、开启数字逻辑的精密运算,测量其支点上,有关效应、常数、一个小目标,精准的给出,使自己提前知道未来取胜的结果。(提前知道一组组数字代码中,给定的“地天代码”数字,就是赢的博文尺度,同时“人天代码”会精准的显示赢了多少。)
博弈圣经著作人的理论学说;国正论的非绝对对立性,相当于“天平两端与支点”类似于“杠杆两端与支点”量化成四两拨千斤“粒湍体博文代码”;⑧1000-4668091=3047.6000(+-*÷)的精确运算,建立的人工智能,他使计算机开始模仿博弈取胜的智慧;
三维支点感知、
三维支点思考、
三维支点意念、
它在三维支点上,进行的数码逻辑运算给出了三个结果;
支点常数加1,结果小于1为神学,(人天代码加地码4000斤+1(-5000斤)=-1000斤);
支点常数加1,结果大于1为科学,(人天代码加地码4000斤+1(5000斤)=+9000斤);
天人代码能够被地码整除(30000斤÷5000斤),天人代码又能被地人代码减、下余一个小数为支点常数(效应、一个小目标)它的结果一定要小于1为博学,(30000斤-26000斤=4000斤)。
博弈取胜的人工智能,“粒湍体博文代码”,是人类认识未知世界,分别计算,神学、科学、博学,使用的数码逻辑法则;
支点常数加1,结果小于1为神学,
支点常数加1,结果大于1为科学,
1除1减,支点常数小于1为博学。
它让每一个人的手指上充满人工智能,点击计算机键盘,体验神学、科学、博学,观赏人与自然博弈的神通,“一人、一指、一键,赢天下”。
3.人工智能是智能算法的实现,其核心内容在于什么?
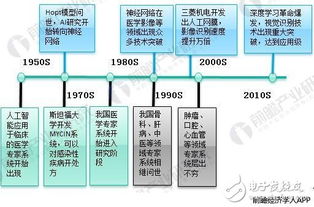
人工智能是计算机学科的一个分支,二十世纪七十年代以来被称为世界三大尖端技术之一(空间技术、能源技术、人工智能)。也被认为是二十一世纪三大尖端技术(基因工程、纳米科学、人工智能)之一。这是因为近三十年来它获得了迅速的发展,在很多学科领域都获得了广泛应用,并取得了丰硕的成果,人工智能已逐步成为一个独立的分支,无论在理论和实践上都已自成一个系统。
人工智能是研究使计算机来模拟人的某些思维过程和智能行为(如学习、推理、思考、规划等)的学科,主要包括计算机实现智能的原理、制造类似于人脑智能的计算机,使计算机能实现更高层次的应用。人工智能将涉及到计算机科学、心理学、哲学和语言学等学科。可以说几乎是自然科学和社会科学的所有学科,其范围已远远超出了计算机科学的范畴,人工智能与思维科学的关系是实践和理论的关系,人工智能是处于思维科学的技术应用层次,是它的一个应用分支。从思维观点看,人工智能不仅限于逻辑思维,要考虑形象思维、灵感思维才能促进人工智能的突破性的发展,数学常被认为是多种学科的基础科学,数学也进入语言、思维领域,人工智能学科也必须借用数学工具,数学不仅在标准逻辑、模糊数学等范围发挥作用,数学进入人工智能学科,它们将互相促进而更快地发展。
4.常用算法算法
在网上找到一篇文章,希望能帮上你的忙 近日导师让偶专门研究了人工智能中的一个经典算法: 有很多感想,写出来与大家共勉,这是上篇: 初识A*算法 A*算法在人工智能中是一种典型的启发式搜索算法,为了说清楚A*算法,我看还是先说 说何谓启发式算法。
一、何谓启发式搜索算法: 在说它之前先提提状态空间搜索。状态空间搜索,如果按专业点的说法就是将问题求解 过程表现为从 初始状态到目标状态寻找这个路径的过程。
通俗点说,就是在解一个问题 时,找到一条解题的过程可以从 求解的开始到问题的结果(好象并不通俗哦)。 由于求 解问题的过程中分枝有很多,主要是求解过程中求 解条件的不确定性,不完备性造成的 ,使得求解的路径很多这就构成了一个图,我们说这个图就是状态空 间。
问题的求解实 际上就是在这个图中找到一条路径可以从开始到结果。这个寻找的过程就是状态空间搜 索。
常用的状态空间搜索有深度优先和广度优先。广度优先是从初始状态一层一层向下找, 直到找到目标 为止。
深度优先是按照一定的顺序前查找完一个分支,再查找另一个分支 ,以至找到目标为止。这两种算 法在数据结构书中都有描述,可以参看这些书得到更详 细的解释。
前面说的广度和深度优先搜索有一个很大的缺陷就是他们都是在一个给定的状态空间中 穷举。这在状 态空间不大的情况下是很合适的算法,可是当状态空间十分大,且不预测 的情况下就不可取了。
他的效率 实在太低,甚至不可完成。在这里就要用到启发式搜索 了。
启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置, 再从这个位置 进行搜索直到目标。这样可以省略大量无畏的搜索路径,提到了效率。
在 启发式搜索中,对位置的估价是 十分重要的。采用了不同的估价可以有不同的效果。
我 们先看看估价是如何表示的。 启发中的估价是用估价函数表示的,如: f(n) = g(n) + h(n) 其中f(n) 是节点n的估价函数,g(n)实在状态空间中从初始节点到n节点的实际代价,h (n)是从n到目 标节点最佳路径的估计代价。
在这里主要是h(n)体现了搜索的启发信息, 因为g(n)是已知的。如果说详细 点,g(n)代表了搜索的广度的优先趋势。
但是当h(n) >> g(n)时,可以省略g(n),而提高效率。这些就深了, 不懂也不影响啦!我们继续看看 何谓A*算法。
二、初识A*算法: 启发式搜索其实有很多的算法,比如:局部择优搜索法、最好优先搜索法等等。当然A* 也是。
这些算法 都使用了启发函数,但在具体的选取最佳搜索节点时的策略不同。象局 部择优搜索法,就是在搜索的过程中 选取“最佳节点”后舍弃其他的兄弟节点,父亲节 点,而一直得搜索下去。
这种搜索的结果很明显,由于舍 弃了其他的节点,可能也把最 好的节点都舍弃了,因为求解的最佳节点只是在该阶段的最佳并不一定是全局 的最佳。 最好优先就聪明多了,他在搜索时,便没有舍弃节点(除非该节点是死节点),在每一 步的估价中 都把当前的节点和以前的节点的估价值比较得到一个“最佳的节点”。
这样 可以有效的防止“最佳节点”的 丢失。那么A*算法又是一种什么样的算法呢?其实A*算 法也是一种最好优先的算法。
只不过要加上一些约束 条件罢了。由于在一些问题求解时 ,我们希望能够求解出状态空间搜索的最短路径,也就是用最快的方法求 解问题,A*就 是干这种事情的!我们先下个定义,如果一个估价函数可以找出最短的路径,我们称之 为可采 纳性。
A*算法是一个可采纳的最好优先算法。A*算法的估价函数克表示为: f'(n) = g'(n) + h'(n) 这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值,h'(n)是n到目标的最断路 经的启发值。
由 于这个f'(n)其实是无法预先知道的,所以我们用前面的估价函数f(n) 做近似。 g(n)代替g'(n),但 g(n)>=g'(n) 才可(大多数情况下都是满足的,可以不用 考虑),h(n)代替h'(n),但h(n) 我们说应用这种估价函数的 最 好优先算法就是A*算法。
哈!你懂了吗?肯定没懂!接着看! 举一个例子,其实广度优先算法就是A*算法的特例。其中g(n)是节点所在的层数,h(n) =0,这种h(n)肯 定小于h'(n),所以由前述可知广度优先算法是一种可采纳的。
实际也 是。当然它是一种最臭的A*算法。
再说一个问题,就是有关h(n)启发函数的信息性。h(n)的信息性通俗点说其实就是在估 计一个节点的值 时的约束条件,如果信息越多或约束条件越多则排除的节点就越多,估 价函数越好或说这个算法越好。
这就 是为什么广度优先算法的那么臭的原因了,谁叫它 的h(n)=0,一点启发信息都没有。但在游戏开发中由于实 时性的问题,h(n)的信息越多 ,它的计算量就越大,耗费的时间就越多。
就应该适当的减小h(n)的信息,即 减小约束 条件。但算法的准确性就差了,这里就有一个平衡的问题。
可难了,这就看你的编程了! 。
5.智能学习算法有哪些
智能计算也有人称之为“软计算”,是们受自然(生物界)规律的启迪,根据其原理,模仿求解问题的算法。
从自然界得到启迪,模仿其结构进行发明创造,这就是仿生学。这是我们向自然界学习的一个方面。
另一方面,我们还可以利用仿生原理进行设计(包括设计算法),这就是智能计算的思想。这方面的内容很多,如人工神经网络技术、遗传算法、模拟退火算法、模拟退火技术和群集智能技术等。
1、人工神经网络算法 “人工神经网络”(ARTIFICIAL NEURAL NETWORK,简称ANN)是在对人脑组织结构和运行机制的认识理解基础之上模拟其结构和智能行为的一种工程系统。早在本世纪40年代初期,心理学家McCulloch、数学家Pitts就提出了人工神经网络的第一个数学模型,从此开创了神经科学理论的研究时代。
其后,F Rosenblatt、Widrow和J. J .Hopfield等学者又先后提出了感知模型,使得人工神经网络技术得以蓬勃发展。 几种典型神经网络简介 1.1 多层感知网络(误差逆传播神经网络) 在1986年以Rumelhart和McCelland为首的科学家出版的《Parallel Distributed Processing》一书中,完整地提出了误差逆传播学习算法,并被广泛接受。
多层感知网络是一种具有三层或三层以上的阶层型神经网络。典型的多层感知网络是三层、前馈的阶层网络,即:输入层I、隐含层(也称中间层)J和输出层K。
相邻层之间的各神经元实现全连接,即下一层的每一个神经元与上一层的每个神经元都实现全连接,而且每层各神经元之间无连接。 但BP网并不是十分的完善,它存在以下一些主要缺陷:学习收敛速度太慢、网络的学习记忆具有不稳定性,即:当给一个训练好的网提供新的学习记忆模式时,将使已有的连接权值被打乱,导致已记忆的学习模式的信息的消失。
1.2 竞争型(KOHONEN)神经网络 它是基于人的视网膜及大脑皮层对剌激的反应而引出的。神经生物学的研究结果表明:生物视网膜中,有许多特定的细胞,对特定的图形(输入模式)比较敏感,并使得大脑皮层中的特定细胞产生大的兴奋,而其相邻的神经细胞的兴奋程度被抑制。
对于某一个输入模式,通过竞争在输出层中只激活一个相应的输出神经元。许多输入模式,在输出层中将激活许多个神经元,从而形成一个反映输入数据的“特征图形”。
竞争型神经网络是一种以无教师方式进行网络训练的网络。它通过自身训练,自动对输入模式进行分类。
竞争型神经网络及其学习规则与其它类型的神经网络和学习规则相比,有其自己的鲜明特点。在网络结构上,它既不象阶层型神经网络那样各层神经元之间只有单向连接,也不象全连接型网络那样在网络结构上没有明显的层次界限。
它一般是由输入层(模拟视网膜神经元)和竞争层(模拟大脑皮层神经元,也叫输出层)构成的两层网络。两层之间的各神经元实现双向全连接,而且网络中没有隐含层。
有时竞争层各神经元之间还存在横向连接。竞争型神经网络的基本思想是网络竞争层各神经元竞争对输入模式的响应机会,最后仅有一个神经元成为竞争的胜者,并且只将与获胜神经元有关的各连接权值进行修正,使之朝着更有利于它竞争的方向调整。
神经网络工作时,对于某一输入模式,网络中与该模式最相近的学习输入模式相对应的竞争层神经元将有最大的输出值,即以竞争层获胜神经元来表示分类结果。这是通过竞争得以实现的,实际上也就是网络回忆联想的过程。
除了竞争的方法外,还有通过抑制手段获取胜利的方法,即网络竞争层各神经元抑制所有其它神经元对输入模式的响应机会,从而使自己“脱颖而出”,成为获胜神经元。除此之外还有一种称为侧抑制的方法,即每个神经元只抑制与自己邻近的神经元,而对远离自己的神经元不抑制。
这种方法常常用于图象边缘处理,解决图象边缘的缺陷问题。 竞争型神经网络的缺点和不足:因为它仅以输出层中的单个神经元代表某一类模式。
所以一旦输出层中的某个输出神经元损坏,则导致该神经元所代表的该模式信息全部丢失。 1.3 Hopfield神经网络 1986年美国物理学家J.J.Hopfield陆续发表几篇论文,提出了Hopfield神经网络。
他利用非线性动力学系统理论中的能量函数方法研究反馈人工神经网络的稳定性,并利用此方法建立求解优化计算问题的系统方程式。基本的Hopfield神经网络是一个由非线性元件构成的全连接型单层反馈系统。
网络中的每一个神经元都将自己的输出通过连接权传送给所有其它神经元,同时又都接收所有其它神经元传递过来的信息。即:网络中的神经元t时刻的输出状态实际上间接地与自己的t-1时刻的输出状态有关。
所以Hopfield神经网络是一个反馈型的网络。其状态变化可以用差分方程来表征。
反馈型网络的一个重要特点就是它具有稳定状态。当网络达到稳定状态的时候,也就是它的能量函数达到最小的时候。
这里的能量函数不是物理意义上的能量函数,而是在表达形式上与物理意义上的能量概念一致,表征网络状态的变化趋势,并可以依据Hopfield工作运行规则不断进行状态变化,最终能够达到的某个极小值的目标函数。网络收敛就是指能量函数达到极小值。
如果把一个最优化问题的。
6.人工智能算法都有哪些
这是infoq上面最近的文章,说的是蒙特卡洛算法来解围棋问题。
目前比较主流方法,大概就是机器学习和神经网络了。
/cn/presentations/computer-go-monte-carlo-search-and-statistical-learning?utm_source=infoq&utm_medium=videos_homepage&utm_campaign=videos_row2
7.人工智能都学习哪些方面的知识
基于人工智能的发展优势,很多小伙伴都想要在这个领域大展宏图,但摆在面前的三道门槛是需要你逐一攻克的。本文分享一下人工智能入门的三道屏障。
门槛一、数学基础
我们应该了解过,无论对于大数据还是对于人工智能而言,其实核心就是数据,通过整理数据、分析数据来实现的,所以数学成为了人工智能入门的必修课程!
数学技术知识可以分为三大学科来学习:
1、线性代数,非常重要,模型计算全靠它~一定要复习扎实,如果平常不用可能忘的比较多;
2、高数+概率,这俩只要掌握基础就行了,比如积分和求导、各种分布、参数估计等等。
提到概率与数理统计的重要性,因为cs229中几乎所有算法的推演都是从参数估计及其在概率模型中的意义起手的,参数的更新规则具有概率上的可解释性。对于算法的设计和改进工作,概统是核心课程,没有之一。当拿到现成的算法时,仅需要概率基础知识就能看懂,然后需要比较多的线代知识才能让模型高效的跑起来。
3、统计学相关基础
回归分析(线性回归、L1/L2正则、PCA/LDA降维)
聚类分析(K-Means)
分布(正态分布、t分布、密度函数)
指标(协方差、ROC曲线、AUC、变异系数、F1-Score)
显著性检验(t检验、z检验、卡方检验)
A/B测试
门槛二、英语水平
我这里说的英语,不是说的是英语四六级,我们都知道计算机起源于国外,很多有价值的文献都是来自国外,所以想要在人工智能方向有所成就,还是要读一些外文文献的,所以要达到能够读懂外文文献的英语水平。
门槛三、编程技术
首先作为一个普通程序员,C++ / Java / Python 这样的语言技能栈应该是必不可少的,其中 Python 需要重点关注爬虫、数值计算、数据可视化方面的应用。
人工智能入门的三道门槛,都是一些必备的基础知识,所以不要嫌麻烦,打好基础很关键!.
8.人工智能需要学些什么
广义的说,人工智能包含诸多不同的方法,其主旨是让程序像一个智能体一样解决问题。
机器d学习是实现人工智能的一种方法,它不完全依靠预先设计,而是从数据中进行总结,达到模拟记忆、推理的作用。包括诸如支持向量机(SVM)、各类基于决策树的算法(包括Boosting、Bagging、Random Forest等),各类基于人工神经网络的算法(例如简单网络及深度网络等),以及多方法的集成等。
基于人工智能的发展优势,很多小伙伴都想要在这个领域大展宏图,但摆在面前的三道门槛是需要你逐一攻克的。本文千锋给大家分享一下人工智能入门的三道屏障。
门槛一、数学基础我们应该了解过,无论对于大数据还是对于人工智能而言,其实核心就是数据,通过整理数据、分析数据来实现的,所以数学成为了人工智能入门的必修课程!数学技术知识可以分为三大学科来学习:1、线性代数,非常重要,模型计算全靠它~一定要复习扎实,如果平常不用可能忘的比较多;2、高数+概率,这俩只要掌握基础就行了,比如积分和求导、各种分布、参数估计等等。提到概率与数理统计的重要性,因为cs229中几乎所有算法的推演都是从参数估计及其在概率模型中的意义起手的,参数的更新规则具有概率上的可解释性。
对于算法的设计和改进工作,概统是核心课程,没有之一。当拿到现成的算法时,仅需要概率基础知识就能看懂,然后需要比较多的线代知识才能让模型高效的跑起来。
3、统计学相关基础回归分析(线性回归、L1/L2正则、PCA/LDA降维)聚类分析(K-Means)分布(正态分布、t分布、密度函数)指标(协方差、ROC曲线、AUC、变异系数、F1-Score)显著性检验(t检验、z检验、卡方检验)A/B测试门槛二、英语水平我这里说的英语,不是说的是英语四六级,我们都知道计算机起源于国外,很多有价值的文献都是来自国外,所以想要在人工智能方向有所成就,还是要读一些外文文献的,所以要达到能够读懂外文文献的英语水平。门槛三、编程技术首先作为一个普通程序员,C++ / Java / Python 这样的语言技能栈应该是必不可少的,其中 Python 需要重点关注爬虫、数值计算、数据可视化方面的应用。
人工智能入门的三道门槛,都是一些必备的基础知识,所以不要嫌麻烦,打好基础很关键。
相关推荐
声明:本网站尊重并保护知识产权,根据《信息网络传播权保护条例》,如果我们转载的作品侵犯了您的权利,请在一个月内通知我们,我们会及时删除。
蜀ICP备2020033479号-4 Copyright © 2016 学习鸟. 页面生成时间:3.217秒









