必修一整理(高中必修一的知识结构以及要点归纳)

1.高中必修一的知识结构以及要点归纳

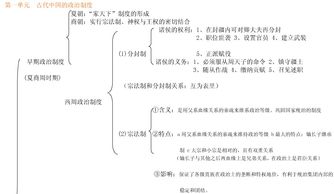
第一单元 古代中国的政治制度第1课 夏、商、西周的政治制度西周的建立——约公元前1046年周武王伐纣灭商，建立周朝。

分封制——目的：巩固周王室的统治 对象：王族、功臣和古代帝王后代。内容： （权利）分封土地和人民给诸侯；诸侯在封国内享有世袭统治权；诸侯可以进行再分封，从而形成了贵族统治阶级内部的森严等级“天子—诸侯—卿大夫—士”。

（义务）服从周天子、镇守疆土、随从作战、交纳贡赋、朝觐述职作用：扩大统治区域、加强周天子对地方的统治。有利于西周政治的稳定，在历史上具有一定的积极意义。

发展： 西周后期，分封制遭到破坏。瓦解原因①生产力发展，井田制瓦解（根本原因）；②诸侯权力的相对独立性大；③周王室衰弱表现： 诸侯争霸和兼并战争不断；诸侯不再听命于周王室，如楚王问鼎；宗法制——（用父系血缘关系的亲疏来维系政治等级、巩固国家统治的制度。）

目的：巩固王权，巩固分封制形成的统治秩序，解决贵族之间在权力、财产和土地继承问题上的矛盾。 特点：嫡长子继承制；大宗和小宗有相对性；血缘关系与政治关系相结合；形成森严等级。

与分封制关系：宗法制是分封制在政治方面的体现，宗法制与分封制相辅相成，互为表里。 作用：宗法制保证了各级贵族在政治上的垄断和特权地位；有利于统治集团内部的稳定和团结。

西周时期政治制度的特点1.王权与神权的紧密结合。 2.以血缘关系为纽带形成国家政治结构（宗法制）3.最高执政集团尚未形成权力的高度集中（分封制） 4.具有相对的延续性（继承性）和稳定性。

第2课 秦中央集权制度的形成专制主义中央集权制度1、含义：（1）专制主义：决策方式，皇帝个人专制独裁，集国家最高权力于一身，从决策到行使权力都有独断性和随意性。 （2）中央集权：地方政府没有独立性，严格服从中央命令，受制于中央。

2、矛盾：（1）君权与相权 （→皇权、中央→君主专制不断强化） （2）中央与地方3、影响：（1）积极：a. 有利统一多民族国家的建立、巩固和发展。B.有利于经济的发展，生产力的提高，民族的融合c. 奠定中华文明长期领先于世界的基础。

d. 有利于抵御外来侵略，维护的完整和统一。 （2）消极：a. 容易形成暴政。

b. 束缚生产力的发展，阻碍了新生产关系的成长。c. 导致思想文化控制的加强，文化专制的日趋严厉，严重阻碍中国科技的发展，阻碍中国文化的发展。

秦朝的统一——历史条件：①人民经受长期分裂和混战，渴望统一②秦国经商鞅变法实力变强③秦王嬴政个人的雄才大略。皇帝的地位及权力：全国的一切大权都由皇帝总揽，中央和地方的主要官员也都由皇帝任免。

皇帝制度建立的影响：在这样的政治体制下，具有独断性和随意性的君主理念，往往影响着政治决策，影响着立法、行政和司法。国家是一个人的国家，政治是一个人的政治。

皇帝制度特征：皇帝独尊、皇位世袭、皇权至上。秦朝的中央机构1.三公的职责——丞相：帮助皇帝处理全国政事；御史大夫：执掌群臣奏章，下达皇帝诏令，并负责监察百官；太尉：负责全国军务（虚设）。

2.三公九卿制特点：分工明确，互不相属，相互牵制，绝对受制于皇帝，大权最后集中在皇帝手中。郡县制——1.郡县制的建立：春秋战国时期，一些诸侯国出现了郡、县。

秦统一后，在全国范围内推行郡县制。2.郡县制的内容：由皇帝直接任免，对上承受中央命令，对下督责所属各县。

不得世袭，没有封地。 郡县制的特点：在于形成了中央垂直管理地方的形式。

3.郡县制建立的影响：是官僚政治取代贵族政治的重要标志，，有利于中央集权的加强和国家统一。秦朝中央集权制度的形成：包括皇帝制度、中央三公九卿制、地方郡县制。

秦朝中央集权制度的作用与社会影响——①彻底打破了传统的贵族分封制，奠定了中国两千多年封建社会政治制度的基本格局。②在中央集权的政治体制下，具有独断性和随意性的君主理念，往往影响着政治决策，影响着立法、行政和司法。

第3课 从汉至元政治制度的演变汉初郡国并行制——西汉初年，刘邦在地方推行郡国并行制；封国有时会有与中央对抗，汉武帝在汉景帝平定“七国之乱”的基础上，颁布“推恩令”，通过分割王国，中央集权得到加强。北宋初年，宋太祖为加强中央集权：①军事上，兵权收归中央，充实中央禁军②行政上，由中央派文官担任地方长官，同时设通判负责监督。

③财政上，地方赋税一小部分作为地方开支，其余全部由中央掌控。 作用：改变了唐末五代以来藩镇割据局面，加强了中央集权。

唐朝三省六部制——皇帝-中书省（草拟、颁发诏令）-门下省（审核政令）-尚书省（执行命令）-吏、户、礼、兵、刑、工评价：①三省相互牵制和监督，保证了君权的独尊②三省分工明确，相互协调，提高了行政效率。元朝的行省制度——元朝中央实行中书省，在地方实行行省制度。

意义：①行省制度便利了中央对地方的管理，加强了中央集权，巩固了多民族国家的统一；②行省制是中国古代地方行政制度重大变革，是中国省制的开端。第4课 明清君主专制的加强明朝废丞相——原因：明太祖认为宰相制度，妨碍了皇权的高度集中，会导致社会。

2.高中数学必修一的知识点总结?

第一章 集合（jihe）与函数概念 一、集合（jihe）有关概念 1、集合的含义：某些指定的对象集在一起就成为一个集合，其中每一个对象叫元素。

2、集合的中元素的三个特性： 1.元素的确定性； 2.元素的互异性； 3.元素的无序性 说明：（1）对于一个给定的集合，集合中的元素是确定的，任何一个对象或者是或者不是这个给定的集合的元素。 （2）任何一个给定的集合中，任何两个元素都是不同的对象，相同的对象归入一个集合时，仅算一个元素。

（3）集合中的元素是平等的，没有先后顺序，因此判定两个集合是否一样，仅需比较它们的元素是否一样，不需考查排列顺序是否一样。 （4）集合元素的三个特性使集合本身具有了确定性和整体性。

3、集合的表示：{ … } 如{我校的篮球队员}，{太平洋，大西洋，印度洋，北冰洋} 1. 用拉丁字母表示集合：A={我校的篮球队员}，B={1,2,3,4,5} 2.集合的表示方法：列举法与描述法。 注意啊：常用数集及其记法： 非负整数集（即自然数集） 记作：N 正整数集 N*或 N+ 整数集Z 有理数集Q 实数集R 关于“属于”的概念 集合的元素通常用小写的拉丁字母表示，如：a是集合A的元素，就说a属于集合A 记作 a∈A ，相反，a不属于集合A 记作 aA 列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。用确定的条件表示某些对象是否属于这个集合的方法。

①语言描述法：例：{不是直角三角形的三角形} ②数学式子描述法：例：不等式x-3>2的解集是{xR| x-3>2}或{x| x-3>2} 4、集合的分类： 1.有限集 含有有限个元素的集合 2.无限集 含有无限个元素的集合 3.空集 不含任何元素的集合 例：{x|x2=-5} 二、集合间的基本关系 1.“包含”关系—子集 注意： 有两种可能（1）A是B的一部分，；（2）A与B是同一集合。 反之： 集合A不包含于集合B，或集合B不包含集合A，记作A B或B A 2.“相等”关系（5≥5，且5≤5，则5=5） 实例：设 A={x|x2-1=0} B={-1,1} “元素相同” 结论：对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时，集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，即：A=B ① 任何一个集合是它本身的子集。

AA ②真子集：如果AB，且A B那就说集合A是集合B的真子集，记作A B（或B A） ③如果 AB, BC ，那么 AC ④ 如果AB 同时 BA 那么A=B 3. 不含任何元素的集合叫做空集，记为Φ 规定： 空集是任何集合的子集， 空集是任何非空集合的真子集。 三、集合的运算 1.交集的定义：一般地，由所有属于A且属于B的元素所组成的集合，叫做A,B的交集. 记作A∩B（读作”A交B”），即A∩B={x|x∈A，且x∈B}. 2、并集的定义：一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A,B的并集。

记作：A∪B（读作”A并B”），即A∪B={x|x∈A，或x∈B}. 3、交集与并集的性质：A∩A = A, A∩φ= φ， A∩B = B∩A,A∪A = A, A∪φ= A ,A∪B = B∪A. 4、全集与补集 （1）补集：设S是一个集合，A是S的一个子集（即 ），由S中所有不属于A的元素组成的集合，叫做S中子集A的补集（或余集） 记作： CSA 即 CSA ={x  xS且 xA} (2)全集：如果集合S含有我们所要研究的各个集合的全部元素，这个集合就可以看作一个全集。通常用U来表示。

（3）性质：⑴CU(C UA)=A ⑵（C UA）∩A=Φ ⑶（CUA）∪A=U 二、函数的有关概念 1.函数的概念：设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f:A→B为从集合A到集合B的一个函数.记作： y=f(x),x∈A.其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域. 注意：○2如果只给出解析式y=f(x)，而没有指明它的定义域，则函数的定义域即是指能使这个式子有意义的实数的集合；○3 函数的定义域、值域要写成集合或区间的形式. 定义域补充 能使函数式有意义的实数x的集合称为函数的定义域，求函数的定义域时列不等式组的主要依据是：（1）分式的分母不等于零； （2）偶次方根的被开方数不小于零； （3）对数式的真数必须大于零；（4）指数、对数式的底必须大于零且不等于1. (5)如果函数是由一些基本函数通过四则运算结合而成的.那么，它的定义域是使各部分都有意义的x的值组成的集合.（6）指数为零底不可以等于零 （6）实际问题中的函数的定义域还要保证实际问题有意义. （又注意：求出不等式组的解集即为函数的定义域。） 2. 构成函数的三要素：定义域、对应关系和值域 再注意：（1）构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的，所以，如果两个函数的定义域和对应关系完全一致，即称这两个函数相等（或为同一函数）（2）两个函数相等当且仅当它们的定义域和对应关系完全一致，而与表示自变量和函数值的字母无关。

相同函数的判断方法：①表达式相同；②定义域一致 （两点必须同时具备） （见课本21页相关例2） 值域补充 （1）、函。

3.高一必修一知识点总结

一， 质点的运动（1）----- 直线运动1）匀变速直线运动1.平均速度V平=S / t （定义式） 2.有用推论Vt 2 –V0 2=2as3.中间时刻速度 Vt / 2= V平=（V t + V o） / 24.末速度V=Vo+at5.中间位置速度Vs / 2=[(V_o2 + V_t2) / 2] 1/26.位移S= V平t=V o t + at2 / 2=V t / 2 t7.加速度a=(V_t - V_o) / t 以V_o为正方向，a与V_o同向（加速）a>0；反向则a8.实验用推论ΔS=aT2 ΔS为相邻连续相等时间（T）内位移之差9.主要物理量及单位：初速（V_o）:m/ s 加速度（a）:m/ s2 末速度（Vt）:m/ s时间（t）：秒（s） 位移（S）：米（m） 路程：米速度单位换算： 1m/ s=3.6Km/ h注：（1）平均速度是矢量。

（2）物体速度大，加速度不一定大。（3）a=(V_t - V_o)/ t只是量度式，不是决定式。

（4）其它相关内容：质点/位移和路程/s--t图/v--t图/速度与速率/2） 自由落体1.初速度V_o =0 2.末速度V_t = g t3.下落高度h=gt2 / 2（从V_o 位置向下计算）4.推论V t2 = 2gh注：（1）自由落体运动是初速度为零的匀加速直线运动，遵循匀变速度直线运动规律。 （2）a=g=9.8≈10m/s2 重力加速度在赤道附近较小，在高山处比平地小，方向竖直向下。

3） 竖直上抛1.位移S=V_o t – gt 2 / 2 2.末速度V_t = V_o – g t (g=9.8≈10 m / s2 )3.有用推论V_t 2 - V_o 2 = - 2 g S 4.上升最大高度H_max=V_o 2 / (2g) （抛出点算起）5.往返时间t=2V_o / g （从抛出落回原位置的时间）注：（1）全过程处理：是匀减速直线运动，以向上为正方向，加速度取负值。（2）分段处理：向上为匀减速运动，向下为自由落体运动，具有对称性。

（3）上升与下落过程具有对称性，如在同点速度等值反向等。平抛运动1.水平方向速度V_x= V_o 2.竖直方向速度V_y=gt3.水平方向位移S_x= V_o t 4.竖直方向位移S_y=gt2 / 25.运动时间t=(2S_y / g)1/2 （通常又表示为（2h/g） 1/2 )6.合速度V_t=(V_x2+V_y2) 1/2=[ V_o2 + (gt)2 ] 1/2合速度方向与水平夹角β： tgβ=V_y / V_x = gt / V_o7.合位移S=(S_x2+ S_y2) 1/2 ，位移方向与水平夹角α： tgα=S_y / S_x=gt / (2V_o)注：（1）平抛运动是匀变速曲线运动，加速度为g，通常可看作是水平方向的匀速直线运动与竖直方向的自由落体运动的合成。

（2）运动时间由下落高度h(S_y)决定与水平抛出速度无关。（3）θ与β的关系为tgβ=2tgα 。

（4）在平抛运动中时间t是解题关键。（5）曲线运动的物体必有加速度，当速度方向与所受合力（加速度）方向不在同一直线上时物体做曲线运动。

2）匀速圆周运动1.线速度V=s / t=2πR / T 2.角速度ω=Φ / t = 2π / T= 2πf3.向心加速度a=V2 / R=ω2 R=(2π/T)2 R 4.向心力F心=mV2 / R=mω2 R=m(2π/ T)2 R5.周期与频率T=1 / f 6.角速度与线速度的关系V=ωR7.角速度与转速的关系ω=2πn （此处频率与转速意义相同）8.主要物理量及单位： 弧长（S）：米（m） 角度（Φ）：弧度（rad） 频率（f）：赫（Hz）周期（T）：秒（s） 转速（n）:r / s 半径（R）：米（m） 线速度（V）:m / s角速度（ω）：rad / s 向心加速度：m / s2注：（1）向心力可以由具体某个力提供，也可以由合力提供，还可以由分力提供，方向始终与速度方向垂直。（2）做匀速度圆周运动的物体，其向心力等于合力，并且向心力只改变速度的方向，不改变速度的大小，因此物体的动能保持不变，但动量不断改变。

3）万有引力1.开普勒第三定律T2 / R3=K(4π2 / GM) R：轨道半径 T ：周期 K：常量（与行星质量无关）2.万有引力定律F=Gm_1m_2 / r2 G=6.67*10-11N•m2 / kg2方向在它们的连线上3.天体上的重力和重力加速度GMm/R2=mg g=GM/R2 R：天体半径（m）4.卫星绕行速度、角速度、周期 V=(GM/R)1/2ω=（GM/R3）1/2 T=2π（R3/GM）1/25.第一（二、三）宇宙速度V_1=(g地r地)1/2=7.9Km/s V_2=11.2Km/s V_3=16.7Km/s6.地球同步卫星GMm / (R+h)2=m4π2 (R+h) / T2h≈36000 km/h：距地球表面的高度注：（1）天体运动所需的向心力由万有引力提供，F心=F万。（2）应用万有引力定律可估算天体的质量密度等。

（3）地球同步卫星只能运行于赤道上空，运行周期和地球自转周期相同。（4）卫星轨道半径变小时，势能变小、动能变大、速度变大、周期变小。

（5）地球卫星的最大环绕速度和最小发射速度均为7.9Km/S。三、力（常见的力、力矩、力的合成与分解）1）常见的力1.重力G=mg方向竖直向下g=9.8 m/s2 ≈10 m/s2 作用点在重心 适用于地球表面附近2.胡克定律F=kX 方向沿恢复形变方向 k：劲度系数（N/m） X：形变量（m）3.滑动摩擦力f=μN 与物体相对运动方向相反 μ：摩擦因数 N：正压力（N）4.静摩擦力0≤f静≤fm 与物体相对运动趋势方向相反 fm为最大静摩擦力5.万有引力F=G m_1m_2 / r2 G=6.67*10-11 N•m2/kg2 方向在它们的连线上6.静电力F=K Q_1Q_2 / r2 K=9.0*109 N•m2/C2 方向在它们的连线上7.电场力F=Eq E：场强N/C q：电量C 正电荷受的电场力与场强方向相同8.安培力F=B I L sinθ θ为B与L的夹角 当 L⊥B时： F=B I L , B//L时： F=09.洛仑兹力f=q V B sinθ θ为B与V的夹角 当V⊥B时： f=q V B , V//B时： f=0注：（1）劲度系数K由弹簧自身决定（2）摩擦因数μ与压力大小及接触面积大小无关，由接触面材料特性与表面状况等决定。

（3）fm略大于μN 一般视为fm≈μN (4)物。

4.高中数学必修1知识点总结

马上就要高考了，现在高中数学让很多孩子头疼，很多的家长还有孩子都开始着急，他们都在上一些辅导班，都在采取一对一的辅导，对于一对一的教师都是可以抓住孩子的一些弱点，然后还要了解他们的学习过程，还会帮助学生制定一些计划，帮助他们提高学习的效率，对于高中数学，一定掌握学习的方法，才可以提高成绩.高中数学都要学习什么知识？

高中数学补习班

一、函数

对于函数这个版块的一些问题，每年都是高考的重点，就想是必修一所学的一些重点就是，集合、定义域、值域以及图像的性质，这些题型在高考数学中是很常见的，对于这些题你们都需要注意哪些事项？

1、集合这个问题还是现在高中数学最基本的一种问题，但是集合这种问题在初中的时候我们就接触过了，现在高中所学的集合也就是在重新讲一下他的概念，让你能很快的完成集合的运算，更重要的一点就是，还可以读懂数学的语言以及他的符号.

2、在初中的时候我们学习函数觉得函数很难，我们初中学的函数，无非就是一些图像还有就是性质，但是高中就不一样了，需要更深入的了解，但是对于复习还是要抓住每一个知识点去进行复习，找到自己的不足，要想提高成绩，就要找到技巧. 二、三角

对于三角，还是经常考的题型，分为三角函数还有就是三角函数的两角之和和之差，对于三角的考查就是要对图像的变化以及性质进行命题，但是这些题，还是很好回答的，只要记住死公式就好.

1、对于解答三角的角度还有就是他们的倍数关系都是可以通过公式进行解答的，这些公式用的比较广泛，实在不会的解答题，还是可以把公式放上去，也要给分.

2、还有半角公式，这个公式还有一定过得范围，会让你来决定，但是在一些表达的式子里面，还要选择和题意一样的.

3、三角函数，我们在初中的时候就接触过，到了高中数学我们还要更深的去了解，还要把一些运算带到高中，一定要掌握技巧.

高中数学知识

对于高中数学的一些知识，其实还是很简单的，只要你抓住学习的方法，从中找到乐趣，让自己喜欢上数学，对你的学习是很有帮助的，至于一对一辅导，其实还是有用的，好的老师会给你讲述好的学习方法，然后让你考一个好成绩，拿到满意的答卷.

5.高中生物必修一基础知识

第一章 走近细胞第一节 从生物圈到细胞一、相关概念、 细 胞：是生物体结构和功能的基本单位。

除了病毒以外，所有生物都是由细胞构成的。细胞是地球上最基本的生命系统 生命系统的结构层次： 细胞→组织→器官→系统（植物没有系统）→个体→种群→群落→生态系统→生物圈二、病毒的相关知识： 1、病毒（Virus）是一类没有细胞结构的生物体。

主要特征：①、个体微小，一般在10~30nm之间，大多数必须用电子显微镜才能看见；②、仅具有一种类型的核酸，DNA或RNA，没有含两种核酸的病毒；③、专营细胞内寄生生活；④、结构简单，一般由核酸（DNA或RNA）和蛋白质外壳所构成。 2、根据寄生的宿主不同，病毒可分为动物病毒、植物病毒和细菌病毒（即噬菌体）三大类。

根据病毒所含核酸种类的不同分为DNA病毒和RNA病毒。 3、常见的病毒有：人类流感病毒（引起流行性感冒）、SARS病毒、人类免疫缺陷病毒（HIV）[引起艾滋病（AIDS）]、禽流感病毒、乙肝病毒、人类天花病毒、狂犬病毒、烟草花叶病毒等。

第二节 细胞的多样性和统一性一、细胞种类：根据细胞内有无以核膜为界限的细胞核，把细胞分为原核细胞和真核细胞二、原核细胞和真核细胞的比较： 1、原核细胞：细胞较小，无核膜、无核仁，没有成形的细胞核；遗传物质（一个环状DNA分子）集中的区域称为拟核；没有染色体，DNA 不与蛋白质结合，；细胞器只有核糖体；有细胞壁，成分与真核细胞不同。 2、真核细胞：细胞较大，有核膜、有核仁、有真正的细胞核；有一定数目的染色体（DNA与蛋白质结合而成）；一般有多种细胞器。

3、原核生物：由原核细胞构成的生物。如：蓝藻、细菌（如硝化细菌、乳酸菌、大肠杆菌、肺炎双球菌）、放线菌、支原体等都属于原核生物。

4、真核生物：由真核细胞构成的生物。如动物（草履虫、变形虫）、植物、真菌（酵母菌、霉菌、粘菌）等。

三、细胞学说的建立： 1、1665 英国人虎克（Robert Hooke）用自己设计与制造的显微镜（放大倍数为40-140倍）观察了软木的薄片，第一次描述了植物细胞的构造，并首次用拉丁文cella（小室）这个词来对细胞命名。 2、1680 荷兰人列文虎克（A. van Leeuwenhoek），首次观察到活细胞，观察过原生动物、人类精子、鲑鱼的红细胞、牙垢中的细菌等。

3、19世纪30年代德国人施莱登（Matthias Jacob Schleiden） 、施旺（Theodar Schwann）提出：一切植物、动物都是由细胞组成的，细胞是一切动植物的基本单位。这一学说即“细胞学说（Cell Theory）”，它揭示了生物体结构的统一性。

第二章 组成细胞的分子第一节 细胞中的元素和化合物一、1、生物界与非生物界具有统一性：组成细胞的化学元素在非生物界都可以找到 2、生物界与非生物界存在差异性：组成生物体的化学元素在细胞内的含量与在非生物界中的含量明显不同二、组成生物体的化学元素有20多种：三、在活细胞中含量最多的化合物是水（85%-90%）；含量最多的有机物是蛋白质（7%-10%）；占细胞鲜重比例最大的化学元素是O、占细胞干重比例最大的化学元素是C。第二节 生命活动的主要承担者------蛋白质一、相关概念：氨 基 酸：蛋白质的基本组成单位 ，组成蛋白质的氨基酸约有20种。

脱水缩合：一个氨基酸分子的氨基（—NH2）与另一个氨基酸分子的羧基（—COOH）相连接，同时失去一分子水。肽 键：肽链中连接两个氨基酸分子的化学键（—NH—CO—）。

二 肽：由两个氨基酸分子缩合而成的化合物，只含有一个肽键。多 肽：由三个或三个以上的氨基酸分子缩合而成的链状结构。

肽 链：多肽通常呈链状结构，叫肽链。二、氨基酸分子通式： NH2—（R — C H —COOH）三、氨基酸结构的特点：每种氨基酸分子至少含有一个氨基（—NH2）和一个羧基（—COOH），并且都有一个氨基和一个羧基连接在同一个碳原子上（如：有—NH2和—COOH但不是连在同一个碳原子上不叫氨基酸）；R基的不同导致氨基酸的种类不同。

四、蛋白质多样性的原因是：组成蛋白质的氨基酸数目、种类、排列顺序不同，多肽链空间结构千变万化。五、蛋白质的主要功能（生命活动的主要承担者）：① 构成细胞和生物体的重要物质，如肌动蛋白；② 催化作用：如酶；③ 调节作用：如胰岛素、生长激素；④ 免疫作用：如抗体，抗原；⑤ 运输作用：如红细胞中的血红蛋白。

六、有关计算： ① 肽键数 = 脱去水分子数 = 氨基酸数目 — 肽链数 ② 至少含有的羧基（—COOH）或氨基数（—NH2） = 肽链数第三节 遗传信息的携带者------核酸一、核酸的种类：脱氧核糖核酸（DNA）和核糖核酸（RNA）二、核 酸：是细胞内携带遗传信息的物质，对于生物的遗传、变异和蛋白质的合成具有重要作用。三、组成核酸的基本单位是：核苷酸，是由一分子磷酸、一分子五碳糖（DNA为脱氧核糖、RNA为核糖）和一分子含氮碱基组成 ；组成DNA的核苷酸叫做脱氧核苷酸，组成RNA的核苷酸叫做核糖核苷酸。

四、DNA所含碱基有：腺嘌呤（A）、鸟嘌呤（G）和胞嘧啶（C）、胸腺嘧啶（T）RNA所含碱基有：腺嘌呤（A）、鸟嘌呤（G）和胞嘧啶（C）、尿。

6.高中数学必修一知识点归纳

1.幂函数 （1）定义形如y=xα的函数叫幂函数，其中α为常数，在中学阶段只研究α为有理数的情形 2.指数函数和对数函数 （1）定义 指数函数，y=ax(a>0，且a≠1)，注意与幂函数的区别. 对数函数y=logax(a>0，且a≠1). 指数函数y=ax与对数函数y=logax互为反函数. （2）指数函数y=ax(a>0，且a≠1)与对数函数y=logax(a>0，且a≠1)的图象和性质如表1-2. (3)指数方程和对数方程 指数方程和对数方程属于超越方程，在中学阶段只要求会解一些简单的特殊类型指数方程和对数方程，基本思想是将它们化成代数方程来解.其基本类型和解法见表1-3.。

7.高中化学必修1详细的知识点总结

高中化学必修一知识点总结必修1全册基本内容梳理从实验学化学 一、化学实验安全 1、（1）做有毒气体的实验时，应在通风厨中进行，并注意对尾气进行适当处理（吸收或点燃等）。

进行易燃易爆气体的实验时应注意验纯，尾气应燃烧掉或作适当处理。 （2）烫伤宜找医生处理。

（3）浓酸撒在实验台上，先用Na2CO3 （或NaHCO3）中和，后用水冲擦干净。浓酸沾在皮肤上，宜先用干抹布拭去，再用水冲净。

浓酸溅在眼中应先用稀NaHCO3溶液淋洗，然后请医生处理。 （4）浓碱撒在实验台上，先用稀醋酸中和，然后用水冲擦干净。

浓碱沾在皮肤上，宜先用大量水冲洗，再涂上硼酸溶液。浓碱溅在眼中，用水洗净后再用硼酸溶液淋洗。

（5）钠、磷等失火宜用沙土扑盖。 （6）酒精及其他易燃有机物小面积失火，应迅速用湿抹布扑盖。

二.混合物的分离和提纯 分离和提纯的方法 分离的物质 应注意的事项 应用举例 过滤 用于固液混合的分离 一贴、二低、三靠 如粗盐的提纯 蒸馏 提纯或分离沸点不同的液体混合物 防止液体暴沸，温度计水银球的位置，如石油的蒸馏中冷凝管中水的流向 如石油的蒸馏 萃取 利用溶质在互不相溶的溶剂里的溶解度不同，用一种溶剂把溶质从它与另一种溶剂所组成的溶液中提取出来的方法 选择的萃取剂应符合下列要求：和原溶液中的溶剂互不相溶；对溶质的溶解度要远大于原溶剂 用四氯化碳萃取溴水里的溴、碘 分液 分离互不相溶的液体 打开上端活塞或使活塞上的凹槽与漏斗上的水孔，使漏斗内外空气相通。打开活塞，使下层液体慢慢流出，及时关闭活塞，上层液体由上端倒出 如用四氯化碳萃取溴水里的溴、碘后再分液 蒸发和结晶 用来分离和提纯几种可溶性固体的混合物 加热蒸发皿使溶液蒸发时，要用玻璃棒不断搅动溶液；当蒸发皿中出现较多的固体时，即停止加热 分离NaCl和KNO3混合物 三、离子检验 离子 所加试剂 现象 离子方程式 Cl- AgNO3、稀HNO3 产生白色沉淀 Cl-+Ag+=AgCl↓ SO42- 稀HCl、BaCl2 白色沉淀 SO42-+Ba2+=BaSO4↓ 四.除杂 注意事项：为了使杂质除尽，加入的试剂不能是“适量”，而应是“过量”；但过量的试剂必须在后续操作中便于除去。

五、物质的量的单位――摩尔 1.物质的量（n）是表示含有一定数目粒子的集体的物理量。 2.摩尔（mol）： 把含有6.02 *1023个粒子的任何粒子集体计量为1摩尔。

3.阿伏加德罗常数：把6.02 X1023mol-1叫作阿伏加德罗常数。 4.物质的量 = 物质所含微粒数目/阿伏加德罗常数 n =N/NA 5.摩尔质量（M）(1) 定义：单位物质的量的物质所具有的质量叫摩尔质量.（2）单位：g/mol 或 g..mol-1(3) 数值：等于该粒子的相对原子质量或相对分子质量. 6.物质的量=物质的质量/摩尔质量 （ n = m/M ） 六、气体摩尔体积 1.气体摩尔体积（Vm）(1)定义：单位物质的量的气体所占的体积叫做气体摩尔体积.（2）单位：L/mol 2.物质的量=气体的体积/气体摩尔体积n=V/Vm 3.标准状况下， Vm = 22.4 L/mol 七、物质的量在化学实验中的应用 1.物质的量浓度. （1）定义：以单位体积溶液里所含溶质B的物质的量来表示溶液组成的物理量，叫做溶质B的物质的浓度。

（2）单位：mol/L(3)物质的量浓度 = 溶质的物质的量/溶液的体积 CB = nB/V 2.一定物质的量浓度的配制 （1）基本原理：根据欲配制溶液的体积和溶质的物质的量浓度，用有关物质的量浓度计算的方法，求出所需溶质的质量或体积，在容器内将溶质用溶剂稀释为规定的体积，就得欲配制得溶液. （2）主要操作 a.检验是否漏水.b.配制溶液 1计算.2称量.3溶解.4转移.5洗涤.6定容.7摇匀8贮存溶液. 注意事项：A 选用与欲配制溶液体积相同的容量瓶. B 使用前必须检查是否漏水. C 不能在容量瓶内直接溶解. D 溶解完的溶液等冷却至室温时再转移. E 定容时，当液面离刻度线1―2cm时改用滴管，以平视法观察加水至液面最低处与刻度相切为止. 3.溶液稀释：C（浓溶液）？V（浓溶液） =C（稀溶液）？V（稀溶液）一、物质的分类 把一种（或多种）物质分散在另一种（或多种）物质中所得到的体系，叫分散系。被分散的物质称作分散质（可以是气体、液体、固体），起容纳分散质作用的物质称作分散剂（可以是气体、液体、固体）。

溶液、胶体、浊液三种分散系的比较 分散质粒子大小/nm 外观特征 能否通过滤纸 有否丁达尔效应 实例 溶液 小于1 均匀、透明、稳定 能 没有 NaCl、蔗糖溶液 胶体 在1—100之间 均匀、有的透明、较稳定 能 有 Fe(OH)3胶体 浊液 大于100 不均匀、不透明、不稳定 不能 没有 泥水 二、物质的化学变化 1、物质之间可以发生各种各样的化学变化，依据一定的标准可以对化学变化进行分类。 （1）根据反应物和生成物的类别以及反应前后物质种类的多少可以分为： A、化合反应（A+B=AB）B、分解反应（AB=A+B） C、置换反应（A+BC=AC+B） D、复分解反应（AB+CD=AD+CB） (2)根据反应中是否有离子参加可将反应分为： A、离子反应：有离子参加的一类反应。

主要包括复分解反应和有离子参加的氧化还原反应。 B、分子反应（非离子反应） （3）根据反应中是否有电子转移可将反应分为： A、氧化还原反应：反应中有电子转移（得失。

8.高一数学必修一知识点总结

第一章 集合与函数概念一、集合有关概念 1、集合的含义：某些指定的对象集在一起就成为一个集合，其中每一个对象叫元素。

2、集合的中元素的三个特性： 1.元素的确定性； 2.元素的互异性； 3.元素的无序性 说明：（1）对于一个给定的集合，集合中的元素是确定的，任何一个对象或者是或者不是这个给定的集合的元素。 （2）任何一个给定的集合中，任何两个元素都是不同的对象，相同的对象归入一个集合时，仅算一个元素。

（3）集合中的元素是平等的，没有先后顺序，因此判定两个集合是否一样，仅需比较它们的元素是否一样，不需考查排列顺序是否一样。 （4）集合元素的三个特性使集合本身具有了确定性和整体性。

3、集合的表示：{ „ } 如{我校的篮球队员}，{太平洋，大西洋，印度洋，北冰洋} 1. 用拉丁字母表示集合：A={我校的篮球队员}，B={1,2,3,4,5} 2.集合的表示方法：列举法与描述法。 注意：常用数集及其记法： 非负整数集（即自然数集） 记作：N 正整数集 N*或 N+ 整数集Z 有理数集Q 实数集R 关于“属于”的概念 集合的元素通常用小写的拉丁字母表示，如：a是集合A的元素，就说a属于集合A 记作 a∈A ，相反，a不属于集合A 记作 a A 列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。用确定的条件表示某些对象是否属于这个集合的方法。

①语言描述法：例：{不是直角三角形的三角形} ②数学式子描述法：例：不等式x-3>2的解集是{x R| x-3>2}或{x| x-3>2} 4、集合的分类： 1.有限集 含有有限个元素的集合 2.无限集 含有无限个元素的集合 3.空集 不含任何元素的集合 例：{x|x2=-5} 二、集合间的基本关系 1.“包含”关系—子集 注意：BA有两种可能（1）A是B的一部分，；（2）A与B是同一集合。 反之： 集合A不包含于集合B，或集合B不包含集合A，记作AB或BA 2.“相等”关系（5≥5，且5≤5，则5=5）实例：设 A={x|x2-1=0} B={-1,1} “元素相同” 结论：对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时，集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，即：A=B ① 任何一个集合是它本身的子集。

A A ②真子集：如果A B，且A B那就说集合A是集合B的真子集，记作AB（或BA） ③如果 A B, B C ，那么 A C ④ 如果A B 同时 B A 那么A=B 3. 不含任何元素的集合叫做空集，记为Φ 规定： 空集是任何集合的子集， 空集是任何非空集合的真子集。 三、集合的运算 1.交集的定义：一般地，由所有属于A且属于B的元素所组成的集合，叫做A,B的交集. 记作A∩B（读作"A交B"），即A∩B={x|x∈A，且x∈B}. 2、并集的定义：一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A,B的并集。

记作：A∪B（读作"A并B"），即A∪B={x|x∈A，或x∈B}. 3、交集与并集的性质：A∩A = A, A∩φ= φ， A∩B = B∩A,A∪A = A,A∪φ= A ,A∪B = B∪A. 4、全集与补集 （1）补集：设S是一个集合，A是S的一个子集（即SA），由S中所有不属于A的元素组成的集合，叫做S中子集A的补集（或余集） 记作： CSA 即 CSA ={x x S且 x A} (2)全集：如果集合S含有我们所要研究的各个集合的全部元素，这个集合就可以看作一个全集。通常用U来表示。

（3）性质：⑴CU(C UA)=A ⑵（C UA）∩A=Φ ⑶（CUA）∪A=U 二、函数的有关概念 1.函数的概念：设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f:A→B为从集合A到集合B的一个函数.记作： y=f(x),x∈A.其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域. 注意：○2如果只给出解析式y=f(x)，而没有指明它的定义域，则函数的定义域即是指能使这个式子有意义的实数的集合；○3 函数的定义域、值域要写成集合或区间的形式. 定义域补充 能使函数式有意义的实数x的集合称为函数的定义域，求函数的定义域时列不等式组的主要依据是：（1）分式的分母不等于零； （2）偶次方根的被开方数不小于零； （3）对数式的真数必须大于零；（4）指数、对数式的底必须大于零且不等于1. (5)如果函数是由一些基本函数通过四则运算结合而成的.那么，它的定义域是使各部分都有意义的x的值组成的集合.（6）指数为零底不可以等于零 （7）实际问题中的函数的定义域还要保证实际问题有意义. （注意：求出不等式组的解集即为函数的定义域。） 构成函数的三要素：定义域、对应关系和值域 再注意：（1）构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的，所以，如果两个函数的定义域和对应关系完全一致，即称这两个函数相等（或为同一函数）（2）两个函数相等当且仅当它们的定义域和对应关系完全一致，而与表示自变量和函数值的字母无关。

相同函数的判断方法：①表达式相同；②定义域一致 （两点必须同时具备）值域补充 （1）、函数的值域取决于定。