粒度分析知识基础(粒度测试的基本知识)

1.粒度测试的基本知识

① 表格法：用表格的方法将粒径区间分布、累计分布一一列出的方法。

② 图形法：在直角标系中用直方图和曲线等形式表示粒度分布的方法。③ 函数法：用数学函数表示粒度分布的方法。

这种方法一般在理论研究时用。如著名的Rosin-Rammler分布就是函数分布。

粒径就是颗粒直径。这概念是很简单明确的，那么什么是等效粒径呢，粒径和等效粒径有什么关系呢？我们知道，只有圆球体才有直径，其它形状的几何体是没有直径的，而组成粉体的颗粒又绝大多数不是圆球形的，而是各种各样不规则形状的，有片状的、针状的、多棱状的等等。

这些复杂形状的颗粒从理论上讲是不能直接用直径这个概念来表示它的大小的。而在实际工作中直径是描述一个颗粒大小的最直观、最简单的一个量，我们又希望能用这样的一个量来描述颗粒大小，所以在粒度测试的实践中的我们引入了等效粒径这个概念。

等效粒径是指当一个颗粒的某一物理特性与同质的球形颗粒相同或相近时，我们就用该球形颗粒的直径来代表这个实际颗粒的直径。那么这个球形颗粒的粒径就是该实际颗粒的等效粒径。

等效粒径具体有如下几种：① 等效体积径：与实际颗粒体积相同的球的直径。一般认为激光法所测的直径为等效体积径。

② 等效沉速径：在相同条件下与实际颗粒沉降速度相同的球的直径。沉降法所测的粒径为等效沉速径，又叫Stokes径。

③ 等效电阻径：在相同条件下与实际颗粒产生相同电阻效果的球形颗粒的直径。库尔特法所测的粒径为等效电阻径。

④ 等效投进面积径：与实际颗粒投进面积相同的球形颗粒的直径。显向镜法和图像法所测的粒径大多是等效投影面积直径。

① D50：一个样品的累计粒度分布百分数达到50%时所对应的粒径。它的物理意义是粒径大于它的颗粒占50%，小于它的颗粒也占50%,D50也叫中位径或中值粒径。

D50常用来表示粉体的平均粒度。② D97：一个样品的累计粒度分布数达到97%时所对应的粒径。

它的物理意义是粒径小于它的的颗粒占97%。D97常用来表示粉体粗端的粒度指标。

其它如D16、D90等参数的定义与物理意义与D97相似。③ 比表面积：单位重量的颗粒的表面积之和。

比表面积的单位为m2/kg或cm2/g。比表面积与粒度有一定的关系，粒度越细，比表面积越大，但这种关系并不一定是正比关系。

同一个样品多次测量结果之间的偏差。重复性指标是衡量一个粒度测试仪器和方法好坏的最重要的指标。

它的计算方法是：其中，n为测量次数（一般n>=10）;x i为每次测试结果的典型值（一般为D50值）；x为多次测试结果典型值的平均值；σ为标准差；δ为重复性相对误差。影响粒度测试重复性有仪器和方法本身的因素；样品制备方面的因素；环境与操作方面的因素等。

粒度测试应具有良好的重复性是对仪器和操作人员的基本要求。 通常的测量仪器都有准确性方面的指标。

由于粒度测试的特殊性，通常用真实性来表示准确性方面的含义。由于粒度测试所测得的粒径为等效粒径，对同一个颗粒，不同的等效方法可能会得到不同的等效粒径。

可见，由于测量方法不同，同一个颗粒得到了两个不同的结果。也就是说，一个不规则形状的颗粒，如果用一个数值来表示它的大小时，这个数值不是唯一的，而是有一系列的数值。

而每一种测试方法的都是针对颗粒的某一个特定方面进行的，所得到的数值是所有能表示颗粒大小的一系列数值中的一个，所以相同样品用不同的粒度测试方法得到的结果有所不同的是客观原因造成的。颗粒的形状越复杂，不同测试方法的结果相差越大。

但这并不意味着粒度测试结果可以漫无边际，而恰恰应具有一定的真实性，就是应比较真实地反映样品的实际粒度分布。真实性目前还没有严格的标准，是一个定性的概念。

但有些现象可以做为测试结果真实性好坏的依据。比如仪器对标准样的测量结果应在标称值允许的误差范围内；经粉碎后的样品应比粉粉碎前更细；经分级后的样品的大颗粒含量应减少；结果与行业标准或公认的方法一致等。

2.粒度分析的作图

粒度分析的结果，可按表6-3所示的格式整理，然后作出直方图、频率曲线图、累积曲线图和概率累积曲线图（图6-5，图6-6）。

图的横坐标表示颗粒大小，纵坐标表示百分数或累积百分数。直方图是广泛使用的一种粒度分布的图解形式，以并排高低不同的矩形表示各粒级百分比。

如果把每个矩形顶连点连接成一平滑曲线，即成频率曲线图。可以一目了然地表示出粒级分布的范围和各粒级的百分比以及百分比最高和最低的粒级所在位置。

缺点是如果粒度数据很多时，很难对比。表6-3 粒度分析资料统计表累积曲线是粒度分析必做的最简单的基础图。

从累积曲线分布的粒级范围和曲线的陡缓，可对沉积物的粒级分布范围、粒度粗细和分选好坏等主要的粒度特征得到直观的感性认识；不同沉积物的累积曲线可绘在一张图上，便于互相对比；可以直接从曲线上读出一些参数，并识别出沉积条件。因此，它是粒度分析中应用很广泛的方法。

图6-5 由直方图所作的频率曲线图6-6 三种常见的粒度曲线用正态概率纸（图6-7）所作的概率累积曲线图，从直观看，概率坐标不是等间距的，中央部分百分比之间的间距小，上下始末两端百分比之间的间距大。其变化规律是以中央50%处为对称中心点，向上下两端相对应地逐渐加大，因而使沉积物的粗细尾端百分含量较小的部分得以放大，使原来在半对数纸上的“S”形累积曲线的始末两端曲线拉长而成为一直线。

所以在正态概率纸上，表示粒度分布的累积百分比图形是由几段相交的直线段组成。不同性质沉积物，线段的数目、交切点和斜度等性质均有不同，便于直观地比较沉积物之间的差别和辨别沉积环境，也可以直接从图上识别不同的搬运与沉积作用。

同时，由于概率累积曲线的粗细尾端变化明显，便于求出φ5、φ16、φ84、φ95的分位数值，利用图算法计算出各种参数。

3.粒径分析仪

原发布者：异域死魂

实验16激光粒度分析中山大学理工学院材料物理实验室中山大学物理实验教学中心材料物理实验室实验目的了解粒度测试的基本知识和基本方法了解激光粒度分析的基本原理和特点掌握用激光粒度分析仪测定粒度和粒度分布的方法中山大学物理实验教学中心材料物理实验室实验原理一、粒度测试的基本知识颗粒：在一定尺寸范围内具有特定形状的几何体。这里所说的一定尺寸一般在毫米到纳米之间，颗粒不仅指固体颗粒，还有雾滴、油珠等液体颗粒。粉体：由大量的不同尺寸的颗粒组成的颗粒群。粒度：颗粒的大小叫做颗粒的粒度。粒度分布：用特定的仪器和方法反映出的不同粒径颗粒占粉体总量的百分数。有区间分布和累计分布两种形式。区间分布又称为微分分布或频率分布，它表示一系列粒径区间中颗粒的百分含量。累计分布也叫积分分布，它表示小于或大于某粒径颗粒的百分含量。遮光比：指测量用的照明光束被测量中的样品颗粒阻挡的部分与照明光的比值，颗粒在测量介质中的浓度中山大学物理实验教学中心材料物理实验室一、粒度测试的基本知识粒度分布的表示方法：表格法：用表格的方法将粒径区间分布、累计分布一一列出的方法。图形法：在直角标系中用直方图和曲线等形式表示粒度分布的方法。函数法：用数学函数表示粒度分布的方法。这种方法一般在理论研究时用。如著名的Rosin-Rammler分布就是函数分布。中山大学物理实验教学中心材料物理实验室一、粒度测试

4.粒度测试的基本方法

粒度测试的方法很多，据统计有上百种。

目前常用的有沉降法、激光法、筛分法、图像法和电阻法五种，另外还有几种在特定行业和领域中常用的测试方法。 沉降法是根据不同粒径的颗粒在液体中的沉降速度不同测量粒度分布的一种方法。

它的基本过程是把样品放到某种液体中制成一定浓度的悬浮液，悬浮液中的颗粒在重力或离心力作用下将发生沉降。不同粒径颗粒的沉降速度是不同的，大颗粒的沉降速度较快，小颗粒的沉降速度较慢。

那么颗粒的沉降速度与粒径有怎样的数量关系，通过什么方式反映颗粒的沉降速度呢？① Stokes定律：在重力场中，悬浮在液体中的颗粒受重力、浮力和粘滞阻力的作用将发生运动，其运动方程为：这就是Stokes定律。从Stokes 定律中我们看到，沉降速度与颗粒直径的平方成正比。

比如两个粒径比为1:10的颗粒，其沉降速度之比为1:100，就是说细颗粒的沉降速度要慢很多。为了加快细颗粒的沉降速度，缩短测量时间，现代沉降仪大都引入离心沉降方式。

在离心沉降状态下，颗粒的沉降事度与粒度的关系如下：这就是Stokes定律在离心状态下的表达式。由于离心转速都在数百转以上，离心加速度ω2r远远大于重力加速度g,Vc>>V，所以在粒径相同的条件下，离心沉降的测试时间将大大缩短。

② 比尔定律：如前所述，沉降法是根据颗粒的沉降速度来测试粒度分布的。但直接测量颗粒的沉降速度是很困难的。

所以在实际应用过程中是通过测量不同时刻透过悬浮液光强的变化率来间接地反映颗粒的沉降速度的。那么光强的变化率与粒径之间的关系又是怎样的呢？比尔是律告诉我们：设在T1、T2、T3、……Ti时刻测得一系列的光强值I1<I2<I3……D2>D3>……>Di，将这些光强值和粒径值代入式（5），再通过计算机处理就可以得到粒度分布了。

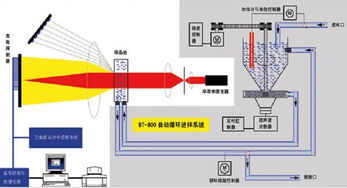
激光法是根据激光照射到颗粒后，颗粒能使激光产生衍射或散射的现象来测试粒度分布的。由激光器的发生的激光，经扩束后成为一束直径为10mm左右的平行光。

在没有颗粒的情况下该平行光通过富氏透镜后汇聚到后焦平面上。如下图所示：当通过适当的方式将一定量的颗粒均匀地放置到平行光束中时，平行光将发生散现象。

一部分光将与光轴成一定角度向外传播。如下图：那么，散射现象与粒径之间有什么关系呢？理论和实验都证明：大颗粒引发的散射光的角度小，颗粒越小，散光与轴之间的角度就越大。

这些不同角度的散射光通过富姓氏透镜后在焦平面上将形成一系列有不同半径的光环，由这些光环组成的明暗交替的光斑称为Airy斑。Airy斑中包含着丰富粒度信息，简单地理解就是半径大的光环对应着较小的粒径；半径小的光环对应着较大的粒径；不同半径的光环光的强弱，包含该粒径颗粒的数量信息。

这样我们在焦平面上放置一系列的光电接收器，将由不同粒径颗粒散射的光信号转换成电信号，并传输到计算机中，通过米氏散理论对这些信号进行数学处理，就可以得到粒度分布了。 电阻法又叫库尔特法，是由美国一个叫库尔特的人发明的一种粒度测试方法。

这种方法是根据颗粒在通过一个小微孔的瞬间，占据了小微孔中的部分空间而排开了小微孔中的导电液体，使小微孔两端的电阻发生变化的原理测试粒度分布的。小孔两端的电阻的大小与颗粒的体积成正比。

当不同大小的粒径颗粒连续通过小微孔时，小微孔的两端将连续产生不同大小的电阻信号，通过计算机对这些电阻信号进行处理就可以得到粒度分布了。如图所示：用库尔特法进行粒度测试所用的介质通常是导电性能较好的生理盐水。

光阻法（Light Blockage），又称为光障碍法或光遮挡法，是利用微粒对光的遮挡所发生的光强度变化进行微粒粒径检测的方法，检测范围从1μm到2.5mm。工作原理：当液体中的微粒通过一窄小的检测区时，与液体流向垂直的入射光，由于被不溶性微粒所阻挡，从而使传感器输出信号变化，这种信号变化与微粒的截面积成正比，光阻法检查注射液中不溶性微粒即依据此原理。

显微图像法包括显微镜、CCD摄像头（或数码像机）、图形采集卡、计算机等部分组成。它的基本工作原理是将显微镜放大后的颗粒图像通过CCD摄像头和图形采集卡传输到计算机中，由计算机对这些图像进行边缘识别等处理，计算出每个颗粒的投影面积，根据等效投影面积原理得出每个颗粒的粒径，再统计出所设定的粒径区间的颗粒的数量，就可以得到粒度分布了。

由于这种方法单次所测到的颗粒个数较少，对同一个样品可以通过更换视场的方法进行多次测量来提高测试结果的真实性。除了进行粒度测试之外，显微图像法还常用来观察和测试颗粒的形貌。

除了上述几种粒度测试方法以外，目前在生产和研究领域还常用刮板法、沉降瓶法、透气法、超声波法和动态光散射法等。（1） 刮板法：把样品刮到一个平板的表面上，观察粗糙度，以此来评价样品的粒度是否合格。

此法是涂料行业采用的一种方法。是一个定性的粒度测试方法。

（2） 沉降瓶法：它的原理与前后讲的沉降法原理大致相同。测试过程是首先将一定量的样品与液体在500ml或1000l的量筒里配制成悬浮液，充分搅拌均匀后取出一定。

5.激光粒度分析仪的基本概念有哪些

粒度分析的基本概念

(1)颗粒：具有一定尺寸和形状的微小物体，是组成粉体的基本单元。它宏观很小，但微观却包含大量的分子和原子；

(2)粒度：颗粒的大小；

(3)粒度分布：用一定的方法反映出一系列不同粒径颗粒分别占粉体总量的百分比；

(4)粒度分布的表示方法：表格法（区间分布和累积分布）、图形法、函数法，常见的有R-R分布，正态分布等；

(5)粒径：颗粒的直径，一般以微米为单位；

(6)等效粒径：指当一个颗粒的某一物理特性与同质球形颗粒相同或相近时，我们就用该球形颗粒的直

径来代表这个实际颗粒的直径；

(7)D10，累计分布百分数达到10% 所对应的粒径值；

D50，累计分布百分数达到50%时所对应的粒径值；又称中位径或中值粒径；

D90，累计分布百分数达到90%时所对应的粒径值；

D(4,3)体积或质量粒径平均值；

常用的粒度测量方法

(1)筛分法

(2)沉降法（重力沉降法、离心沉降法）

(3)电阻法（库尔特颗粒计数器）

(4)显微镜（图像）法

(5)电镜法

(6)超声波法

(7)透气法

(8)激光衍射法

各种方法的优缺点

筛分法：优点：简单、直观、设备造价低、常用于大于40μm的样品。缺点：不能用于40μm以细的样品；结果受人为因素和筛孔变形影响较大。

显微镜法：优点：简单、直观、可进行形貌分析。 缺点：速度慢、代表性差，无法测超细颗粒。

沉降法（包括重力沉降和离心沉降）：优点：操作简便，仪器可以连续运行，价格低，准确性和重复性较好，测试范围较大。 缺点：测试时间较长。

电阻法：优点：操作简便，可测颗粒总数，等效概念明确，速度快，准确性好。 缺点：测试范围较小，小孔容易被颗粒堵塞，介质应具备严格的导电特性。

电镜法：优点：适合测试超细颗粒甚至纳米颗粒、分辨率高。 缺点：样品少、代表性差、仪器价格昂贵。

超声波法：优点：可对高浓度浆料直接测量。 缺点：分辨率较低。

透气法：优点：仪器价格低，不用对样品进行分散，可测磁性材料粉体。 缺点：只能得到平均粒度值，不能测粒度分布。

激光法：优点：操作简便，测试速度快，测试范围大，重复性和准确性好，可进行在线测量和干法测量。 缺点：结果受分布模型影响较大

6.粒径分析仪

激光粒度分析仪原理和特点 2004年12月29日16时15分 慧聪网激光光电子行业 激光粒度分析仪原理 光在传播中，波前受到与波长尺度相当的隙孔或颗粒的限制，以受限波前处各元波为源的发射在空间干涉而产生衍射和散射，衍射和散射的光能的空间（角度）分布与光波波长和隙孔或颗粒的尺度有关。

用激光做光源，光为波长一定的单色光后，衍射和散射的光能的空间（角度）分布就只与粒径有关。对颗粒群的衍射，各颗粒级的多少决定着对应各特定角处获得的光能量的大小，各特定角光能量在总光能量中的比例，应反映着各颗粒级的分布丰度。

按照这一思路可建立表征粒度级丰度与各特定角处获取的光能量的数学物理模型，进而研制仪器，测量光能，由特定角度测得的光能与总光能的比较推出颗粒群相应粒径级的丰度比例量。 激光粒度分析仪 采用湿法分散技术，机械搅拌使样品均匀散开，超声高频震荡使团聚的颗粒充分分散，电磁循环泵使大小颗粒在整个循环系统中均匀分布，从而在根本上保证了宽分布样品测试的准确重复。

测试操作简便快捷：放入分散介质和被测样品，启动超生发生器使样品充分分散，然后启动循环泵，实际的测试过程只有几秒钟。测试结果以粒度分布数据表、分布曲线、比表面积、D10、D50、D90等方式显示、打印和记录. 输出数据丰富直观：本仪器的软件可以在各种计算机视窗平台上运行，具有操作简单直观的特点，不仅对样品进行动态检测，而且具有强大的数据处理与输出功能，用户可以选择和设计最理想的表格和图形输出。

7.粒度分布特征及其环境意义

沉积物的颗粒大小称为粒度。

研究碎屑沉积物和碎屑岩的粒度大小和各种粒级的分布特征的方法称为粒度分析。粒度分布特征可反映沉积介质的流体力学性质和能量，故是判别沉积环境及水动力条件的一个重要物理标志，而且对于油气沉积储层的评价也有重要意义。

碎屑物质以机械搬运为主，其搬运和沉积作用是受水动力条件（如介质、流量、流速）控制的，碎屑物质埋藏后除部分石英有次生加大或溶解外，一般颗粒变化不大。因此，粒度大小及分布特征，可用来直接反映沉积时的水动力条件。

研究粒度分布，可提供如下资料：①明确搬运介质性质，如风、水、冰川、泥石流、浊流等；②判断搬运介质的能量条件，如流速、强度、启动能力等；③明确搬运方式，如滚动、跳跃、悬浮；④明确沉积作用的形式，如牵引流、浊流等。（一）粒度分析的主要方法根据颗粒大小及岩石致密程度不同，分别采用如下三种方法。

1.直接测量法一般用于砾岩或砾石，其方法是用度量工具直接测量砾石的直径或视直径大小，一般测量一定面积内的全部砾石（粒径大于2 mm的颗粒）不少于100个，用于河流、滨海、冰川、洪积等砾岩的分析。2.筛析法用于未固结或胶结较差的含砾砂岩到粉砂岩，它是用一套筛孔直径不同的筛子将砂样过筛，以分成不同的粒级组分，一般筛孔直径按1/4Φ间隔选择较好，称出每层筛内砂的质量，并求出其百分含量。

筛析法比较简便，也较精确，注意取样应在一个完整层序内，粗、中、细砂均应取样。3.薄片粒度法一般用于较致密的岩石，其方法是在显微镜下，用测微尺直接测量岩石薄片中颗粒的最大视直径，并将测量值换算成Φ值，按1/4间隔分组，计算各组内颗粒百分数，每片要求统计300~500颗粒。

运用上述不同的方法所得到的分析结果可能有偏差，如薄片粒度与筛析粒径之间的偏差可达0.25Φ或更大，这是切片效应造成的结果（切片效应是指在颗粒集合体的切片中，颗粒的视直径均小于其真直径），必须进行校正，弗里德曼（1962）提出的粒度回归校正方程是：D=0.3815+0.9027d(D为校正后筛析直径Φ值；d为薄片中视直径Φ值)。在运用薄片粒度法进行粒度分析时还必须考虑砂岩中基质的影响，即进行杂基校正，方法是用显微镜测定或估出杂基含量，由于切片效应和成岩后生作用，其值一般较高，取其2/3或1/2为校正值，假定为X，将各累计频率乘以（100-X）作为该粒级的真正百分含量。

（二）颗粒粒级的划分一般采用伍登 温特沃思标准，它是以毫米（mm）为单位的一个分类方案，后来克鲁宾（1934）提出了一种对数换算，称其为Φ值（Φ=-log2D，其中D为颗粒直径）。粒径（mm）和Φ值的对应关系见表5-4。

（三）粒度曲线和粒度参数根据粒度分析的结果，可编制各种直方图、粒度曲线及计算各种粒度参数。1.直方图和粒度曲线直方图和粒度曲线都是沉积环境分析的参考标志。

常用的粒度曲线包括直方图、频率曲线、累积曲线、概率累积曲线。直方图 是最常用的粒度分析图件，其横坐标为颗粒粒径区间，纵坐标表示粒级的百分含量，作出一系列相互连接、高低不平的矩形图（图5-30左），直方图优点是能直观、简明地反映出粒度分布特征。

表5-4 粒级划分标准比较表频率曲线 是将直方图每个柱子的纵、横边的中点依次连成多边形频率曲线（图5-30右），其围限的多边形的面积仍基本等于直方图的面积和。频率曲线可清楚地表明粒度分布特点、分选好坏、粒度分布的对称度（偏度）及尖度（峰度）等。

图5-30 由直方图所作频率曲线（据克鲁莫艾尼塔尔，1938）累积曲线 是一种常用的简单的图形，它是以累积百分含量为纵坐标，以粒径为横坐标，从粗粒一端开始，在图上标出每一粒级的累计百分含量。将各点以圆滑的曲线连接起来，即成累积曲线（图5-31）。

累积曲线一般呈S型，从图上可看出其粒级分选的好坏，在计算粒度参数时也可由图上读出某些累计百分比对应的粒径值。累积曲线的形态，可用来区分不同的沉积环境。

概率累积曲线 也是一种粒度累积曲线，它是在正态概率纸上绘制的，横坐标代表粒径；纵坐标为累积百分数，并以概率标度，概率坐标不是等间距的，而是以50%处为对称中心，上下两端相应地逐渐加大，这样可以将粗、细尾部放大，并清楚地表现出来。概率曲线中碎屑沉积物的粒度不是一个简单的对数正态分布，而是由几个呈对数正态分布的次总体组成，一般包含有三个次总体，在概率图上表现为三个直线段，代表了三种不同的基本搬运方式，即悬浮搬运、跳跃搬运和滚动搬运（图5-32）。

三个次总体在累积概率曲线上分别称为悬浮总体、跳跃总体和滚动总体（牵引总体），概率图上除三个次总体之外的其他参数有：截点、混合度、次总体百分含量、分选性。图5-31 三种常见的粒度曲线（据赖内克等，1973）1—频率曲线；2—累积曲线；3—概率累积曲线图5-32 概率累积曲线及粒度分布中的总体（据维谢尔，1969）截点，指两个次总体直线的交点，以横坐标表示，细截点（S截点）是悬浮总体和跳跃总体的交点，表示能悬浮的最粗颗粒；粗截点（T截点）是跳动总体和滚动总体的交点，表示能跳跃的最粗颗粒。

混。

8.粒度的检测方法

浅谈粒度计算张 铃安徽大学人工智能研究所230039摘要：粒度计算是新近兴起的人工智能研究领域的一个方向，本文简单介绍粒度计算的主要三个方法，以及之间的关系。

关键词：粒度计算、模糊逻辑、商空间理论、粗糙集理论。一. 引言人们在思考问题时，或者是先从总体进行观察，然后再逐步深入地研究各个部分的情况；或先从各个方面对同一问题进行不同侧面的了解，然后对它们进行综合；或是上面两种方法的组合，即时而从各侧面对事物进行了解，然后进行综合观察，时而综合观察后，对不甚了解的部分再进行观察……总之，根据需要从不同侧面、不同角度反复对事物进行了解、分析、综合、推理.最后得出事物本质的性质和结论.人工智能研究者对人类这种能力进行了深入地研究，并建立了各种形式化的模型.本文要介绍的粒度计算，就是对上述问题的研究的一个方面.人工智能最主要的目的是，为人类的某些智能行为建立适当的形式化模型，以便利用计算机能再显人的智能的部分功能。

什么是人类的最主要的智能，或者说智能的最重要表现形式是什么。各家有不同的看法，如Simon等认为人的智能表现为，对问题求解目标的搜索（Search）能力。

比如学生在证明一道平面几何题目时，进行思考，“聪明的小孩”能很快地找到证明该结论的有关的定理性质，并很快地应用上去，从而就得到证明。“数学能力差的学生”可能东找西寻，找不到合适的定理和性质，绕来绕去，总得不到证明的要领；Pawlak[P1]则认为人的智能表现为对事物（事件、行为、感知等）的分类（Classification）能力。

如平时我们说某医生本事大，就是这位医生能从病人的症状中，正确地诊断出病人是患什么病（分类能力！分出患什么病来）等等。我们认为“人类智能的公认特点，就是人们能从极不相同的粒度（Granularity）上观察和分析同一问题。

人们不仅能在不同粒度的世界上进行问题求解，而且能够很快地从一个粒度世界跳到另一个粒度的世界，往返自如，毫无困难。这种处理不同世界的能力，正是人类问题求解的强有力的表现”[ZH1]。

还有很多不同的理解，人们正是从这些不同的理解分别建立各自的模型和相关的理论和方法。粒度计算目前国际上有三个主要的模型和方法，下面简单进行介绍。

二. 三种不同的模型下面简单介绍有关“粒度计算”的三个不同的模型和方法。什么是粒度，顾名思义，就是取不同大小的对象。

也就是说，将原来“粗粒度”的大对象分割为若干“细粒度”的小对象，或者把若干小对象合并成一个大的粗粒度对象，进行研究。最近Zadeh在[ZA1]-[ZA3]中，讨论模糊信息粒度理论时，提出人类认知的三个主要概念，即粒度（granulation）、组织（organization）、因果（causation）（粒度包括将全体分解为部分，组织包括从部分集成为全体，因果包括因果的关联）。

并进一步提出粒度计算。他认为，粒度计算是一把大伞它覆盖了所有有关粒度的理论、方法论、技术和工具的研究。

指出：“粗略地说，粒度计算是模糊信息粒度理论的超集，而粗糙集理论和区间计算是粒度数学的子集”。Zadeh 的工作激起了学术界对粒度计算研究的兴趣，Y.Y.Yao和他的合作者对粒度计算进行了一系列的研究[Y1]-[Y3]并将它应用于数据挖掘等领域，其工作的要点是用决策逻辑语言（DL-语言）来描述集合的粒度（用满足公式元素的集合，来定义等价类m（）），建立概念之间的IF-THEN关系与粒度集合之间的包含关系的联系，并提出利用由所有划分构成的格，来求解一致分类问题。

这些研究为知识挖掘提供了一些新的方法和角度。按Zadeh粒度计算的定义，我们提出的商空间理论和Pawlak的粗糙集理论都属于“粒度计算”范畴。

目前有关粒度计算的理论与方法，主要有三个。一是Zadeh的“词计算理论”（Theory of Works Computing），一是Pawlak的“粗糙集理论”（Theory of Rough Set），另一个是我们提出的“商空间理论”（Theory of Quotient Space）。

下面简单介绍三者的内容：1. 词计算理论：Zadeh认为人类在进行思考、判断、推理时主要是用语言进行的，而语言是一个很粗的“粒度”，如我们说“九寨沟的风景很美”，其中“很美”这个词就比较“庞统”，也就是说其粒度很粗，如何利用语言进行推理判断，这就是要进行“词计算”，早在二十世纪六十年代Zadeh提出模糊集理论，就是“词计算”的雏型。沿Zadeh的模糊集论的方向，用模糊数学的方法进行有关粒度计算的方法和理论的研究，就构成“粒度计算”的一个非常重要的方法和方向。

这也是人们比较熟悉的一个方法。2. 粗糙集理论：波兰学者Pawlak[P1]在二十世纪八十年代，提出的粗糙集理论，他提出一个假设：人的智能（知识）就是一种分类的能力，这个假设可能不是很完备，但却非常精练。

在此基础上提出，概念可以用论域中的子集来表示，于是在论域中给定一组子集族，或说给定一个划分（所谓划分，是指将X分成两两不相交的子集之并）。从数学上知道，给定X上的一个划分，等价于在X上给定一个等价关系R。

Pawlak称之为在论域上给定了一个知识基（X,R）。然后讨论一个一般的概念x(X中的一个子。