基础术数知识(周易中的术数是什么内容?)

1.周易中的术数是什么内容?

中国术数，简称术数，泛指在中华文化中用以推算未来、趋吉避凶的各种方术系统。

术数分类：山 医 命 卜 相。

术数以卜筮、风水、命理、占梦等各种型态的预知方法，推算对象由人、事物、家居、先人墓地，以至地运、国运不等。术数的原理基本是易经的八卦与阴阳五行。

包括风水、八字、命理、大六壬、奇门遁甲、太乙神数、梅花易数、紫微斗数等。

“术数”也可写做“数术”。

“术”→ 古代原意是指道路，后引申为方法，技术；

“数”→ 对事物的量的规定。

“术数”中方法，技术首先指巫术，以及带有巫术性质的神秘主义的方法和技术。

所以说你这样问是不准确的，术数不完全是《周易》，《周易》中占卜或者说象数的部分才能叫术数。

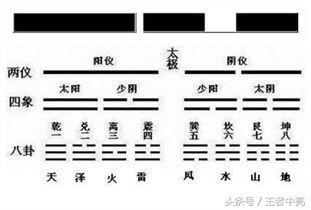
2.数术的基本概念

古人将自然界所观察到的各种变化，与人事、政治、社会的变化结合起来，认为两者有某种内在关系，这种关系可用术数来归纳、推理。于是，术数便用来推测个人，甚至国家的命运吉凶。《黄帝内经-素问-上古天真论》：“上古之人，其知道者，法于阴阳，和于术数。”《汉书-艺文志》将天文、历谱、五行、蓍龟、杂占、形法等六方面列入术数范围。《中国方术大辞典》把凡是运用这种阴阳五行生克制化的数理以行占卜之术的，皆纳入术数范围。如：星占、卜筮、六壬、奇门遁甲、相命、拆字、起课、堪舆、择日等等。 目前常见的比较有影响力及体系比较完整的术数门类有以下几种：八字术、相术、风水术、姓名学、紫微斗数、星相学、择吉、六爻预测术、奇门遁甲、大六壬等。

八字术：也叫“四柱推命术”，源于唐朝李虚中的禄命术，宋朝徐子平所发明，故也叫“子平术”。是一种用于测算个人命运的方术。其法是将人出生的年、月、日、时各配以天干和地支，这样，描述一个人的生辰就刚好用了八个字。这是一种将人出生的时间转换成干支，再在干支中带入阴阳五行系统而进行复杂运算的一种算命术（这种运算不是我们常用的“加减乘除”而是“生克制化”）。八字术在中国大陆地区仍然是民间流传最广的一种命术。 相术：相术细分有面相、手相、骨相、体相、乳相、声相等等相术。在中国大陆地区，相术在民间的普及程度几乎不下于八字术。 风水术：因强调“避风藏水”之用而得名，在古代也叫“堪舆术”或“地理学”。如果说八字术、相术等是一种卜命的方术的话，风水术则是一种造命的方术。其中又分为“阳宅术”与“阴宅术”两大应用门类。阳宅术是看活人住宅吉凶，帮人选屋的。阴宅术则是看死人坟墓，帮人选坟地的。当然，其中还有很多诀窍，如利用开门、换房，养鱼、引水，植树等方式来改变人的运气。 紫微斗数：名列五大神数之首，号称“天下第一神数”。古代生于五代宋初的陈抟受当时的五星术的启发而创，故形式上颇为接近当时的五星术（内在机理可能完全不同），但更为简洁、直观，使用操作也更为方便（如将十干化曜简化为四化星，化圆图为方图，省略五星历等等）。但由于难解的原因，此术创后一直沉没，直到明朝嘉靖年间始得刊行，但亦未能普及，直到上世纪70年代才在台湾逐渐兴盛起来，并与90年代初回传至中国大陆，至今在国内习者日增，影响日大。 星相学：中国古代叫“五星术”或“七政四馀占星术”，西方叫“星辰学”，现在台湾人叫“星宗”。是利用人出生时的刹那间宇宙天体的位置来测算人命运的一种术数。最初这种术数只是用来占卜军国大事、社会变迁，最后才发展成为了一种预测个人命运的术数。由于源自西方的星座书的普及，现在星相学中一些基础东西（如黄道十二星座）已被年轻人普遍接受，而其深奥的部分也研究者日众。 择吉：选择吉日良辰以办事的一种术数。如选择结婚吉日、出行吉日、开业吉日、丧葬吉日等等。包括有九星择日术、十二黄道择日、二十八宿择日、乌兔太阳经择日法及十二执择日法等方法及流派。择吉在古代非常受重视，在现代渐趋没落。 六爻预测术：或叫“纳甲筮法”，是易经发展到后期的一个产物。也可说是易经的一个分支和具体应用门类。主要用于占卜具体事件而不是算命。与之相似的还有一个同是易经发展起来的术数叫“梅花易数”，梅花易数由为其起卦及断卦方法不易确定较难掌握和运用，故习者较少。

姓名学：最流行的一个流派是“五格剖象法”，这是近代由日本人发明，80年代后期传入中国的。它依据姓名的笔画数，而且取的是繁体的笔画数，强调笔画数对人产生的吉凶影响，通常是和八字配合使用的。另外还有“音灵姓名学”，强调姓名的读音对人产生的吉凶影响。此外还有强调字形的“字形姓名学”和将姓名笔画数转换成易卦用易经卦爻来解释吉凶的“易卦姓名学”。（这是从性质上来进行分类的，实际上除五格剖象法外其它名称并无统一的说法，甚至有些“大师”把上面列举的其中几种折衷一下，自己给它按个名，就“创造”出一种新的姓名学出来）。 奇门遁甲：“古传三式”之一。也是一种预测具体事件的术数。和六爻预测术相比，除了对时间的重视外，它还重视空间和方位的作用，因此它可算得上是一种比较立体的术数。 大六壬：“古传三式”之一，也是一种占卜术。

3.术数的具体内容是什么?术数的具体内容是什么?

术数基本上都从《易经》衍生而来，包括山、医、命、相、卜。

（1）山一一道家追求身心健康的养生之法具体分为：食饵（通过日常饮食和补药治病健体），筑基（通过修禅、静坐养气健体），玄典（以老庄思想修身养性），拳法（通过练习各种武术强身健体），符咒（以通灵和修炼辟邪镇煞）。 （2） 医——中医治病救人、保持健康之法具体分为：方剂（通过散剂和丸剂治疗疾病），针灸（通过针法和灸法治疗疾病），灵治（通过调整心态状态治疗疾病）等。

（3） 命一-古人占卜凶吉、推命改命之法具体分为：紫微斗数（利用星曜和天干地支判断吉凶），四柱预测（利用天干地支、五行八字的生克刑冲关系推演命运），星平会海（以月亮、太阳为中心推演八字）。 （4） 相——古人观形知义、趋利避害之法具体分为：印相（以观看人的印章判断命 运的方法），名相（以人的姓名或店铺的名 称，通过五格剖相判断凶吉），人相（通过观察面、手部的纹线与气色而了解人的吉凶、病理），家相（以阳宅的风水推断居所的吉凶），墓相（通过选地安葬祖先，而达到对后代子孙的荫庇）。

（5） 卜——古人占卜起卦、预测吉凶之法具体分为：奇门遁甲（以布局、布斗、符咒等方式指挥军事），梅花易数（通过数理推断事件发展吉凶），太乙神数（以十二运卦象推算国家政治前景），测字（解拆字判断吉凶），占梦（解析梦境判断吉凶）。 。

4.什么是术数,术数是什么意思

这个词其实百度百科中有解释，我不需要复制，下面我手打下我自己的见解来说说。

个人认为，术数就是指以易经理论为基础，包括或含有阴阳、五行、六亲、天干地支等各种文字符号成立的易经类的子学科。

说直白点，八字、六爻、大六壬、奇门盾甲、风水等等都算是易经的子学科，也是我们常指的术数学，术数学包括他们，但他们如八字和六爻又是不同的学科体系，但都需要运用术数学的知识比如阴阳五行天干地支。

再用现代人能理解的话就是，术数就类似于数学。而会计、测量、微积分、函数等都是建立在数学上的子学科，这样能明白了吗？

5.术数分哪些种,大致用处?

占卜方法从用途上可以分为命术和卦术两大类

命术用来解读命运，卦术用来解答具体事件

从流派上讲

东方的术较强的两支主要是印度和中国，印度是以佛学以及梵我合一的自然观的占卜方式，主要精于命术，主流是印度占星术，中国主要是以阴阳哲学，五行生克关系，易经的卦象变化，以及天干地支类象学为基础的众多术。目前常用命术在民间主要就行的有的有子平术，紫微斗数，邵字神数，铁板神术，七政四余等。卦术较为丰富，民间常用的有纳甲（六爻）术，梅花易数，小成图，河洛神术，三式神学（太乙，奇门遁甲，大六壬），较为特殊的以前两者为基础的还有风水学，包括八宅派，玄空飞星，玄空大卦，三合派等众多流派，另有一些边缘应用学科，如释梦学，姓名学，相学等

西洋的主流方法有星相学，生命灵数，塔罗三种，另有一些如灵摆，如尼石，色彩瓶等非主流方法。

6.怎样入手学习古代术数

我也想了解古代术数

术数包括风水、八字、命理、大六壬、奇门遁甲、太乙神数、梅花易数、紫微斗数等

它包含的方面太多了，先选个你最感兴趣的专一学吧，古代的知识感觉和新派命理又有不同甚至抵触额==+

周易，我倒是买了哦，但是根本看不进去。。没买好，买了本太死了的书，我看到有人推荐张志春老师的《神奇之门》和《开悟之门》。本人并没有亲自看过，仅告诉你借鉴借鉴额。

不过可以从周易上了解一些简单基础的东西，八卦什么的

感觉不买点什么书，看点真实案例，听点专人讲座，确实不能明白额。。。==+

7.想多了解一些关于术数方面的知识,什么书比较好

关于术数的书很多，学习也不是件简单的事情，很需要对一些内容进行背诵。

介绍两本我感觉比较重要的书：

《易经》 这本书是术数的一个基础，断卦很多时候都要依靠它，如果是有师傅教的话，一般这本书是要求必背的。背下来，理解透，才能对卦象有比较好的理解，不至于断错卦。

《梅花易数》 这是一本比较经典的起卦书。内容比较通俗易懂，有些内容也需要硬背，记的清楚才能想的明白。

我曾自己摸索自己学习这方面的知识，感觉没有师傅自己学习是比较困难的。若要学的好，一方面是下苦工硬背，这是基础；另外悟性也很重要，对文字的理解要透彻，最好还是找师傅教，呵呵。

8.《易经》中何谓术数

术，指法术，简单理解就是方式方法。

数，指理数、气数，就是运用方法时的规律， 即阴阳五行生克制化的运动规律。术数，作 为中华传统文化的重要组成部分，曾一度成 为我国历史上社会生活中的时尚，但其内涵 和外延至今仍不清晰，学术界并未给出确切 的划分。

术数的起源，则是曾经在古代盛行一时的巫术。诸如天文.历法、数学、星占、太乙、奇门、运气、占候、卜筮、命理、相 法、择吉、养生术、房中术等都属术数范畴。

一般来讲，狭义的术数，专指预测吉凶的一 种法术，泛指在中华文化中用来推算未来、趋吉避凶的一切方术系统。

9.术数算法的历史及发展

1 中国古代数学的发展 在古代世界四大文明中，中国数学持续繁荣时期最为长久。

从公元前后至公元14世纪，中国古典数学先后经历了三次发展高潮，即两汉时期、魏晋南北朝时期和宋元时期，并在宋元时期达到顶峰。 与以证明定理为中心的希腊古典数学不同，中国古代数学是以创造算法特别是各种解方程的算法为主线。

从线性方程组到高次多项式方程，乃至不定方程，中国古代数学家创造了一系列先进的算法（中国数学家称之为“术”），他们用这些算法去求解相应类型的代数方程，从而解决导致这些方程的各种各样的科学和实际问题。特别是，几何问题也归结为代数方程，然后用程式化的算法来求解。

因此，中国古代数学具有明显的算法化、机械化的特征。以下择要举例说明中国古代数学发展的这种特征。

1.1 线性方程组与“方程术” 中国古代最重要的数学经典《九章算术》（约公元前2世纪）卷8的“方程术”，是解线性方程组的算法。以该卷第1题为例，用现代符号表述，该问题相当于解一个三元一次方程组： 3x+2y+z=39 2x+3y+z=34 x+2y+3z=26 《九章》没有表示未知数的符号，而是用算筹将xyz的系数和常数项排列成一个（长）方阵： 1 2 3 2 3 2 3 1 1 26 34 39 “方程术”的关键算法叫“遍乘直除”，在本例中演算程序如下：用右行（x）的系数（3）“遍乘”中行和左行各数，然后从所得结果按行分别“直除”右行，即连续减去右行对应各数，就将中行与左行的系数化为0。

反复执行这种“遍乘直除”算法，就可以解出方程。很清楚，《九章算术》方程术的“遍乘直除” 算法，实质上就是我们今天所使用的解线性方程组的消元法，以往西方文献中称之为“高斯消去法”，但近年开始改变称谓，如法国科学院院士、原苏黎世大学数学系主任P.Gabriel教授在他撰写的教科书[4]中就称解线性方程组的消元法为“张苍法”，张苍相传是《九章算术》的作者之一。

1.2 高次多项式方程与“正负开方术” 《九章算术》卷4中有“开方术”和“开立方术”。《九章算术》中的这些算法后来逐步推广到开更高次方的情形，并且在宋元时代发展为一般高次多项式方程的数值求解。

秦九韶是这方面的集大成者，他在《数书九章》（1247年）一书中给出了高次多项式方程数值解的完整算法，即他所称的“正负开方术”。 用现代符号表达，秦九韶“正负开方术”的思路如下：对任意给定的方程 f(x)=a[0]x^n+a[1]x^(n-1)+……+a[n-2]x^2+a[n-1]x+a[n]=0 (1) 其中a[0]≠0,a[n]<0，要求（1）式的一个正根。

秦九韶先估计根的最高位数字，连同其位数一起称为“首商”，记作c，则根x=c+h，代入（1）得 f(c+h)=a[0](c+h)^n+a[1](c+h)^(n-1)+……+a[n-1](c+h)+a[n]=0 按h的幂次合并同类项即得到关于h的方程： f(h)=a[0]h^n+a[1]h^(n-1)+……+a[n-1]h+a[n]=0 (2) （注：这里（2）和（1）式子里的a，一般是不一样的。） 于是又可估计满足新方程（2）的根的最高位数字。

如此进行下去，若得到某个新方程的常数项为0，则求得的根是有理数；否则上述过程可继续下去，按所需精度求得根的近似值。 如果从原方程（1）的系数a[0],a[1]，…，a[n]及估值c求出新方程（2）的系数a[0],a[1]，…，a[n]的算法是需要反复迭代使用的，秦九韶给出了一个规格化的程序，我们可称之为“秦九韶程序”，他在《数书九章》中用这一算法去解决各种可以归结为代数方程的实际问题，其中涉及的方程最高次数达到10次，秦九韶解这些问题的算法整齐划一，步骤分明，堪称是中国古代数学算法化、机械化的典范。

1.3 多元高次方程组与“四元术” 绝不是所有的问题都可以归结为线性方程组或一个未知量的多项式方程来求解。实际上，可以说更大量的实际问题如果能化为代数方程求解的话，出现的将是含有多个未知量的高次方程组。

多元高次方程组的求解即使在今天也绝非易事。历史上最早对多元高次方程组作出系统处理的是中国元代数学家朱世杰。

朱世杰的《四元玉鉴》（1303年）一书中涉及的高次方程达到了4个未知数。朱世杰用“四元术”来解这些方程。

“四元术”首先是以“天”、“地”、“人”、“物”来表示不同的未知数，同时建立起方程式，然后用顺序消元的一般方法解出方程。朱世杰在《四元玉鉴》中创造了多种消元程序。

通过《四元玉鉴》中的具体例子可以清晰地了解朱世杰“四元术”的特征。值得注意的是，这些例子中相当一部分是由几何问题导出的。

这种将几何问题转化为代数方程并用某种统一的算法求解的例子，在宋元数学著作中比比皆是，充分反映了中国古代几何代数化和机械化的倾向。 1.4 一次同余方程组与“中国剩余定理” 中国古代数学家出于历法计算的需要，很早就开始研究形如： X≡Ri (mod ai) i=1,2,。

,n (1) （其中ai 是两两互素的整数）的一次同余方程组求解问题。公元4世纪的《孙子算经》中已有相当于求解下列一次同余组的著名的“孙子问题”： X≡2(mod3) ≡3(mod5) ≡2(mod7) 《孙子算经》作者给出的解法，引导了宋代秦九韶求解一次同余组的一般算法——“大衍求一术”。

现代文献中通常把这种一般算法称为“中国剩余定理”。 1.5 插值法与“招差术” 插值算法在微积分的酝酿过程。