幂函数高三(求有关幂函数的一切知识)
1.求有关幂函数的一切知识
简介
形如y=x^a(a为常数)的函数，即以底数为自变量 幂为因变量，指数为常量的函数称为幂函数。
当a取非零的有理数时是比较容易理解的，而对于a取无理数时，初学者则不大容易理解了。因此，在初等函数里，我们不要求掌握指数为无理数的问题，只需接受它作为一个已知事实即可，因为这涉及到实数连续统的极为深刻的知识。
编辑本段
特性
对于a的取值为非零有理数，有必要分成几种情况来讨论各自的特性：
首先我们知道如果a=p/q，且p/q为既约分数（即p、q互质），q和p都是整数，则x^(p/q)=q次根号下（x的p次方），如果q是奇数，函数的定义域是R，如果q是偶数，函数的定义域是[0，+∞）。当指数a是负整数时，设a=-k，则y=1/(x^k)，显然x≠0，函数的定义域是（-∞，0）∪（0，+∞）。因此可以看到x所受到的限制来源于两点，一是有可能作为分母而不能是0，一是有可能在偶数次的根号下而不能为负数，那么我们就可以知道：
排除了为0与负数两种可能，即对于x>0，则a可以是任意[实数；
排除了为0这种可能，即对于x<0或x>0的所有实数，q不[能是偶数；
排除了为负数这种可能，即对于x为大于或等于0的所有实数，a就不能是负数。
编辑本段
定义域
总结起来，就可以得到当a为不同的数值时，幂函数的定义域的不同情况如下：
如果a为任意实数，则函数的定义域为大于0的所有实数；
如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根[据q的奇偶性来确定，即如果同时q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数；如果同时q为奇数，则函数的定义域为不等于0 的所有实数。
在x大于0时，函数的值域总是大于0的实数。
在x小于0时，则只有同时q为奇数，函数的值域为非零的实数。
而只有a为正数，0才进入函数的值域。
由于x大于0是对a的任意取值都有意义的，
因此下面给出幂函数在第一象限的各自情况.
编辑本段
第一象限
可以看到：
(1)所有的图形都通过（1,1）这点.（a≠0） a>0时 图象过点（0,0）和（1,1）
(2)当a大于0时，幂函数为单调递增的，而a小于0时，幂函数为单调递减函数。
(3)当a大于1时，幂函数图形下凸；当a小于1大于0时，幂函数图形上凸。
(4)当a小于0时，a越小，图形倾斜程度越大。
(5)显然幂函数无界限。
(6)a=2n，该函数为偶函数 {x|x≠0}。
(7) 0<a<1时，只在第一象限内有图像，即x≥0.
编辑本段
图象
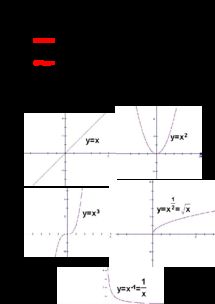
幂函数的图象：
2.高一数学 幂函数 性质 归纳 100分
幂函数y=x^α重点是α=±1，±2，±3，±1/2.
1. α=0.
y=x^0.
图象：过点（1,1），平行于x轴的直线一条（剔去点（0,1）).
定义域：（-∞，0）∪（0，+∞）.
值域：{1}.
奇偶性：偶函数
2. α∈Z+.
①α=1
y=x
图象：过点（1,1），一、三象限的角平分线（包含原点（0,0）).
定义域：（-∞，+∞）.
值域：. （-∞，+∞）
单调性：增函数。
奇偶性：奇函数。
②α=2
y=x^2
图象：过点（1,1），抛物线.
定义域：（-∞，+∞）.
值域：. [0，+∞）
单调性：减区间（-∞，0]，增区间[0，+∞）
奇偶性：偶函数。
注：当α=2n, n∈N+时，幂函数y=x^α也具有上述性质。
③α=3
y=x^3
图象：过点（1,1），立方抛物线.
定义域：（-∞，+∞）.
值域：. （-∞，+∞）
单调性：增函数。
奇偶性：奇函数。
注：当α=2n+1, n∈N+时，幂函数y=x^α也具有上述性质。
3.α是负整数。
①α=-1
y=x^(-1).
图象：过点（1,1），双曲线.
定义域：（-∞，0）∪（0，+∞）.
值域：. （-∞，0）∪（0，+∞）
单调性：减区间（-∞，0）和（0，+∞）。
奇偶性：奇函数。
②α=-2
y=x^(-2)。
图象：过点（1,1），分布在一、二象限的拟双曲线.
定义域：（-∞，0）∪（0，+∞）.
值域：（0，+∞）
单调性：增区间（-∞，0），减区间（0，+∞）
奇偶性：偶函数。
注：当α=-2n, n∈N+时，幂函数y=x^α也具有上述性质。
③α=-3
y=x^(-3)
图象：过点（1,1），双曲线型.
定义域：（-∞，0）∪（0，+∞）.
值域：（-∞，0）∪（0，+∞）
单调性：减区间（-∞，0）和（0，+∞）
奇偶性：奇函数。
注：当α=-2n+1, n∈N+时，幂函数y=x^α也具有上述性质。
4.α是正分数。
①α=1/2.
y=x^(1/2)=√x.
图象：过点（1,1），分布在一象限的抛物线弧（含原点）。
定义域：[0，+∞）.
值域：[ 0，+∞）.
单调性：增函数。
奇偶性：非奇非偶。
注：当α=（2n+1）/(2m), m,n∈N+时，幂函数y=x^α也具有上述性质。
②α=1/3.
y=x^(1/3)
图象：过点（1,1），与立方抛物线y=x^3关于直线y=x对称。.
定义域：（-∞，+∞）.
值域：. （-∞，+∞）.
单调性：增函数。
奇偶性：奇函数。
注：当α=（2n-1）/(2m+1), m,n∈N+时，幂函数y=x^α也具有上述性质。
5.α是负分数。
①α=-1/2.
y=x^(-1/2)=1/√x.
图象：过点（1,1），只分布在一象限的双曲线弧。
定义域：（0，+∞）.
值域：（ 0，+∞）.
单调性：减函数。
奇偶性：非奇非偶。
注：当α=-（2n-1）/(2m), m,n∈N+时，幂函数y=x^α也具有上述性质。
②α=-1/3.
y=x^(-1/3)=1/(3)√x.
图象：过点（1,1），双曲线型。
定义域：（-∞，0）∪（0，+∞）.
值域：（-∞，0）∪（0，+∞）.
单调性：减区间（-∞，0）和（0，+∞）。
奇偶性：奇函数。
注：当α=-（2n-1）/(2m+1), m,n∈N+时，幂函数y=x^α也具有上述性质。
3.高中函数知识点
一、函数的概念与表示
1、映射
(1)映射：设A、B是两个集合，如果按照某种映射法则f，对于集合A中的任一个元素，在集合B中都有唯一的元素和它对应，则这样的对应（包括集合A、B以及A到B的对应法则f）叫做集合A到集合B的映射，记作f:A→B。
注意点：（1）对映射定义的理解。（2）判断一个对应是映射的方法。一对多不是映射，多对一是映射
2、函数
构成函数概念的三要素 ①定义域②对应法则③值域
两个函数是同一个函数的条件：三要素有两个相同
二、函数的解析式与定义域
1、求函数定义域的主要依据：
(1)分式的分母不为零；
(2)偶次方根的被开方数不小于零，零取零次方没有意义；
(3)对数函数的真数必须大于零；
(4)指数函数和对数函数的底数必须大于零且不等于1;
三、函数的值域
1求函数值域的方法
①直接法：从自变量x的范围出发，推出y=f(x)的取值范围，适合于简单的复合函数；
②换元法：利用换元法将函数转化为二次函数求值域，适合根式内外皆为一次式；
③判别式法：运用方程思想，依据二次方程有根，求出y的取值范围；适合分母为二次且 ∈R的分式；
④分离常数：适合分子分母皆为一次式（x有范围限制时要画图）；
⑤单调性法：利用函数的单调性求值域；
⑥图象法：二次函数必画草图求其值域；
⑦利用对号函数
⑧几何意义法：由数形结合，转化距离等求值域。主要是含绝对值函数
四.函数的奇偶性
1.定义： 设y=f(x),x∈A，如果对于任意 ∈A，都有 ，则称y=f(x)为偶函数。
如果对于任意 ∈A，都有 ，则称y=f(x)为奇
函数。
2.性质：
①y=f(x)是偶函数 y=f(x)的图象关于 轴对称， y=f(x)是奇函数 y=f(x)的图象关于原点对称，
②若函数f(x)的定义域关于原点对称，则f(0)=0
③奇±奇=奇 偶±偶=偶 奇*奇=偶 偶*偶=偶 奇*偶=奇[两函数的定义域D1 ,D2,D1∩D2要关于原点对称]
3.奇偶性的判断
①看定义域是否关于原点对称 ②看f(x)与f(-x)的关系
五、函数的单调性
1、函数单调性的定义：
2 设 是定义在M上的函数，若f(x)与g(x)的单调性相反，则 在M上是减函数；若f(x)与g(x)的单调性相同，则 在M上是增函数。
4.高中数学函数部分详细的知识点总结
去百度文库，查看完整内容>
内容来自用户：鍒橀佩宄
《函数》知识要点和基本方法
1.映射定义：设非空集合A,B，若对集合A中任一元素a，在集合B中有唯一元素b与之对应，则称从A到B的对应为映射。若集合A中有m个元素，集合B中有n个元素，则从A到B可建立nm个映射。
2.函数定义：函数就是定义在非空数集A,B上的映射f。此时称数集A为函数f(x)的定义域，集合C={f(x)|x∈A}为值域，且CB。
3.定义域、对应法则和值域构成了函数的三要素。
相同函数的判断方法：①定义域、值域；②对应法则。（两点必须同时具备）
4.求函数的定义域常涉及到的依据为：①分母不为0；②偶次根式中被开方数不小于0；③对数的真数大于0，底数大于零且不等于1；④零指数幂的底数不等于零；⑤实际问题要考虑实际意义；⑥正切函数角的终边不在y轴上。
5.函数解析式的求法：①配凑法；②换元法：③待定系数法；④赋值法；⑤消元法等。
6.函数值域的求法：①配方法；②分离常数法；③逆求法；④换元法；⑤判别式法；⑥单调性法等。
7.函数单调性及证明方法：
如果对于定义域内某个区间上的任意两个自变量的值x1,x2，当x1<x2时，都有f(x1)f(x2)），那么就说f(x)在这个区间上是增函数（或减函数）。
第一步：设x1、x2是给定区间内的两个任意的值，且x1<x2；第二步：作差f(x2)-f(x1)，并对1120②从33例例【题型例6C13415(
