初中锐角三角函数知识点基础题(关于初中数学的二次函数和锐角三角函数的重点难点)
1.关于初中数学的二次函数和锐角三角函数的重点难点
初中数学的二次函数
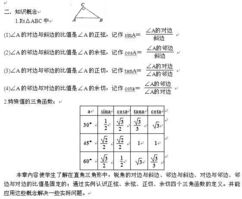
初中数学锐角三角函数知识点总结:
解直角三角形,解直角三角形的知识是近几年各地中考命题的热点之一,考察题型为选择题,填空题,应用题为主,分值一般8-12分,难易度为难。考察内容:①常见锐角的三角函数值的计算,②根据图形计算距离,高度,角度的应用题,③根据题中给出的信息构建图形,建立数学模型,然后用解直角三角形的知识解决问题。突破方法:掌握三角函数的概念,会熟练运用特殊三角函数值,②了解某些问题中的仰角,俯角,坡度等概念,③将实际问题转换为数学问题,建立数学模型④涉及解斜三角形的问题时,会通过作适当的辅助线构造直角三角形,使之转化为直角三角形的计算问题而达到解决实际问题。⑤解应用题的关键是根据实际问题画出是示意图,弄清图中各个量的具体意义及各已知量和未知量的关系。通过大量练习,熟练建模。
2.初三三角函数练习题
1.在△ABC中,AB=AC=10,BC=16,则tanB=3/4______。
2.在RT△ABC中,∠C=90°,AC=12,BC=15.
(1)AB的长=√369=19.2。
(2)sinA=15/19.2、cosA=12/19.2。
(3)sin²A+cos²A=1
(4)sinA=cosB
3.已知锐角α满足tanα=5/12,求sinα和cosα的值。
tanα=sinα/cosα=5/12,12sinα=5cosα
144sin^2α=25cos^2α=25-25sin^2α
sin^2α=25/169
sinα=5/13 , cosα=12/13
4.已知2+√3是方程x²-5xsinθ+1=0的一个根,求sinθ和cosθ。
7+4√3-(10+5√3)sinθ+1=0
sinθ=(8+4√3)/(10+5√3)=4/5
cosθ=3/5
5.已知公式sin(α+β)=sinαcosβ,sin(α-β)=sinαcosβ-cosαsinβ,计算sin75°和cos75°的值。
sin75°=(√2+√6)/4
cos75°=(√6-√2)/4
6.已知sinα=2m-3,且α为锐角,求m的取值范围
2m-3≤1 ,m≤2
3.初三锐角三角函数公式
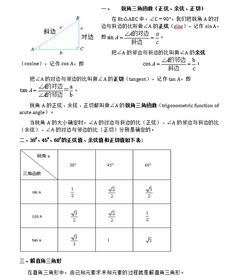
1.1 正弦和余弦 例1 已知0°≤α≤90°.(1)求证:sin2α+cos2α=1; (2)求证:sinα+cosα≥1,讨论在什么情形下等号成立; (3)已知sinα+cosα=1,求sin3α+cos3α的值. 证明 (1)如图6-1,当0°<α<90°时,sinα=BC/AB,cosα=AC/AB,所以在这种情形下 当α=0°时,sinα=0,cosα=1;当α=90°,sinα=1,cosα=0.所以在这两种情形下仍有 sin2α+cos2α=1. (2)如图6-1,当0°<α<90°时,sinα=BC/AB,cosα=AC/AB.所以在这种情形下 当α=0°时,sinα+cosα=0+1=1;当α=90°时,sinα+cosα=1+0=1.所以当0°≤α≤90°时,总有 sinα+cosα≥1, 当并且只当α=0°或α=90°时,等号成立. (3)由于已知sina+cosα=1.由(2)可知α=0°或α=90°,所以总有 sin3α+cos3α=1. 例2 求证:对于0°≤α≤90°, 证法一 如图6-1,设BC=a,AC=b,AB=c.由锐角三角函数 当α=0°或α=90°时,容易验证以上等式仍成立. 证法二 点评 证法一是根据锐角三角函数的定义;证法二用了公式sin2α+cos2α=1. 证明一个三角恒等式成立,可变换等号左(右)端的式子,如得到等号右(左)端的式子,原恒等式就被证明了.一般对较复杂的式子进行变换,也可以对等号左,右的式子都进行变换,如得到相同的式子,原恒等式就被证明了. 1.2 正切和余切 证明 (1)当0°<α<90°时,如图6-2, 当α=0°时,tgα=0,sinα=0,cosα=1.所以仍有tgα= (2)α必须满足不等式: 0°<α<90°. 如图6-2, 所以tgα·ctgα=1. 例2 已知锐角α,且tgα是方程x2-2x-3=0的一个根,求 解法一 x2-2x-3=0的两根为3和-1.这里只能是tgα=3. 如图6-3,由于tgα=3.因此可设BC=3,AC=1,从而 解法二 tgα=3,用cos2α除原式分子,分母,得 证法一 如图6-2,设BC=a,AC=b,AB=c,则 所以原式成立. 证法二 等式的左端 点评 这里α≠0°,90°. 怎样理解锐角三角函数的概念 答:现行初中几何课本中给出锐角三角函数的定义,是依据这样一个基本事实:在直角三角形中,当锐角固定时,它的对边,邻边与斜边的比值是一个固定的值. 关于这点,我们看图1,图中的直角三角形AB1C1,AB2C2,AB3C3,…都有一个相等的锐角A,即锐角A取一个固定值.如图所示,许许多多直角三角形中相等的那个锐角叠合在一起,并使一条直角边落在同一条直线上,那么斜边必然都落在另一条直线上.不难看出, B1C1‖B2C2‖B3C3‖…, ∵△AB1C1∽△AB2C2∽△AB3C3∽…, 因此,在这些直角三角形中,∠A的对边与斜边的比值是一个固定的值. 根据同样道理,由"相似形"知识可以知道,在这些直角三角形中,∠A的对边与邻边的比值,∠A的邻边与斜边的比值都分别是某个固定的值. 这样在△ABC中,∠C为直角,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA;锐角A邻边与斜边的比叫做∠A的余弦,记作cosA;锐角A的对边与邻边的比叫做∠A的正切,记作tgA;锐角A的邻边与对边的比叫做∠A的余切,记作ctgA,于是我们得到锐角A的四个锐角三角函数,即 深刻理解锐角三角函数定义,要注意以下几点: (1)角A的锐角三角函数值与三角形的大小,即边的长短无关. 只要角A一旦确定,四个比值就随之而定;角A变化时.四个比值对应变化.这正体现了函数的特点,锐角三角函数也是一种函数,这里角A是自变量,对于每一个确定的角A,上面四个比值都有唯一确定的值与之对应,因此,锐角三角函数是以角为自变量,以比值为函数值的函数. (2)准确理解锐角三角函数定义,要熟记每个锐角三角函数是怎样规定的,是角的哪条边与哪条边的比;在具体应用定义时,要注意分清图形中,哪条边是角的对边,哪条边是角的邻边,哪条边是斜边. [例] 求出图2中sinD,tgE的值. (3)"sinA"等是一个完整的符号. 整的符号,不能看成sin与A的乘积.离开角A的"sin"没有什么意义,其他三个cosA,tgA,ctgA等也是这样.所以写时不能把"sin"与"A"分开. 锐角三角函数定义把形与数结合起来,从事物的相互联系去观察,对直角三角形不是孤立地看它的角,它的边,而是抓住了它们之间的联系,从而为深入研究问题打开了思路,奠定了基础.从定义的导出过程不难看出,锐角三角函数是数(比值)和形(角A)完美结合的结果,同学们应该在学习中很好地体会和掌握这种研究问题的思想方法. 计算 解答题 3. 在Rt△ABC中,∠C=90°,若sinA是方程5x2 -14x+8=0的一个根,求sinA,tgA. 4. q为三角形的一个角,如果方程10x2-(10cosq)x-3cosq+4=0有两个相等的实数根,求tgq. 答案 3. 解:∵sinA是方程5x2-14x+8=0的一个根 则5sin2A-14sinA+8=0 4. 解:∵100cos2q-40(4-3cosq)=0 即5cos2q+6cosq-8=0。
声明:本网站尊重并保护知识产权,根据《信息网络传播权保护条例》,如果我们转载的作品侵犯了您的权利,请在一个月内通知我们,我们会及时删除。
蜀ICP备2020033479号-4 Copyright © 2016 学习鸟. 页面生成时间:2.715秒









