多元回归方法都(常见的回归分析方法)

1.常见的回归分析方法有哪些

1/6分步阅读

1.线性回归方法：通常因变量和一个（或者多个）自变量之间拟合出来是一条直线（回归线），通常可以用一个普遍的公式来表示：Y（因变量）=a*X（自变量）+b+c，其中b表示截距，a表示直线的斜率，c是误差项。如下图所示。



2/6

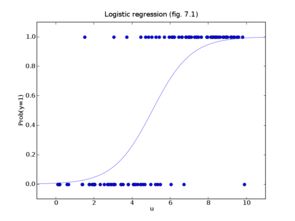
2.逻辑回归方法：通常是用来计算“一个事件成功或者失败”的概率，此时的因变量一般是属于二元型的（1 或0，真或假，有或无等）变量。以样本极大似然估计值来选取参数，而不采用最小化平方和误差来选择参数，所以通常要用log等对数函数去拟合。如下图。



3/6

3.多项式回归方法：通常指自变量的指数存在超过1的项，这时候最佳拟合的结果不再是一条直线而是一条曲线。比如：抛物线拟合函数Y=a+b*X^2，如下图所示。



4/6

4.岭回归方法：通常用于自变量数据具有高度相关性的拟合中，这种回归方法可以在原来的偏差基础上再增加一个偏差度来减小总体的标准偏差。如下图是其收缩参数的最小误差公式。



5/6

5.套索回归方法：通常也是用来二次修正回归系数的大小，能够减小参量变化程度以提高线性回归模型的精度。如下图是其惩罚函数，注意这里的惩罚函数用的是绝对值，而不是绝对值的平方。



6/6

6.ElasticNet回归方法：是Lasso和Ridge回归方法的融合体，使用L1来训练，使用L2优先作为正则化矩阵。当相关的特征有很多个时，ElasticNet不同于Lasso，会选择两个。如下图是其常用的理论公式。



2.常用的多元分析方法

多元分析方法包括3类：

多元方差分析、多元回归分析和协方差分析，称为线性模型方法，用以研究确定的自变量与因变量之间的2113关系；判别函数分析和聚类分析，用以研究对事物的分类；主成分分析、典型相关和因素分析，研究如何用较少的5261综合因素代替为数较多的原始变量。

多元方差是把总变异按照其来源分为多个部分，从而检验各个因素对因变量的影响以及各因素间交互作用的统计方法。

判别函数是判定个体所属类别的统计方法。其基本原理是：根据两个或多个已知类别的样本观测资料确4102定一个或几个线性判别函数和判别指标，然后用该判别函数依据判别指标来判定另一个个体属于哪一类。

扩展资料

多元分析方1653法的历史：

首先涉足多元分析方法是F.高尔顿，他于1889年把双变量的正态分布方法运用于传统的统计学，创立了相关系数和线性回归。

其后的几十年中，斯皮尔曼提出因素分析法，费内希尔提出方差分析和判别分析，威尔克斯发展了多元方差分析，霍特林确定了主成分分析和典型相关。到20世纪前半叶，多元分析理论大多已经确立。

60年代以后，随着计算机科学的发展，多元分析方法在心理学以及其他许多学科的研究中得到了越来越广泛的应用。容

参考资料来源：百度百科——多元分析

3.回归分析法的分类

回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。此外，回归分析中，又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。回归分析法预测是利用回归分析方法，根据一个或一组自变量的变动情况预测与其有相关关系的某随机变量的未来值。进行回归分析需要建立描述变量间相关关系的回归方程。根据自变量的个数，可以是一元回归，也可以是多元回归。根据所研究问题的性质，可以是线性回归，也可以是非线性回归。非线性回归方程一般可以通过数学方法为线性回归方程进行处理。

4.多元线性回归中自变量筛选常用的方法有哪些

筛选变量法， 岭回归分析法， 主成分回归法和偏最小二乘回归法。

关键词： 回归、SASSTAT、共线性、筛选变量、岭回归、主成分回归、偏最小二乘回归。中图分类号： 0212; C8 文献标识码： A 回归分析方法是处理多变量间相依关系的统计方法。

它是数理统计中应用最为广泛的方法之一。在长期的大量的实际应用中人们也发现： 建立回归方程后， 因为自变量存在相关性， 将会增加参数估计的方差， 使得回归方程变得不稳定； 有些自变量对因变量（指标） 影响的显著性被隐蔽起来； 某些回归系数的符号与实际意义不符合等等不正常的现象。

这些问题的出现原因就在于自变量的共线性。本文通过例子来介绍自变量共线性的诊断方法以及使用SA SSTA T 软件6. 12 版本中REG 等过程的增强功能处理回归变量共线性的一些方法。

一、共线性诊断共线性问题是指拟合多元线性回归时， 自变量之间存在线性关系或近似线性关系。共线性诊断的方法是基于对自变量的观测数据构成的矩阵X′X 进行分析， 使用各种反映自变量间相关性的指标。

共线性诊断常用统计量有方差膨胀因子V IF （或容限TOL ）、条件指数和方差比例等。方差膨胀因子V IF 是指回归系数的估计量由于自变量共线性使得其方差增加的一个相对度量。

对第i 个回归系数， 它的方差膨胀因子定义为 V I F i = 第i 个回归系数的方差自变量不相关时第i 个回归系数的方差 = 1 1 - R 2 i = 1 TOL i 其中R 2 i 是自变量xi 对模型中其余自变量线性回归模型的R 平方。V IFi 的倒数TOL i 也称为容限（ To lerance ）。

一般建议， 若V IF> 10， 表明模型中有很强的共线性问题。若矩阵X′X 的特征值为d 2 1 ≥d 2 2 ≥…≥d 2 k， 则X 的条件数 d1 dk 就是刻划它的奇性的一个指标。

故称 d1 dj (j= 1， …， k) 为条件指数。一般认为， 若条件指数值在10 与30 间为弱相关； 在30 与100 间为中等相关； 大于100 表明有强相关。

对于大的条件指数， 还需要找出哪些变量间存在强的线性关系。因为每个条件指数对应一 9 4 处理多元线性回归中自变量共线- 性的几种方法个特征向量， 而大的条件指数相应的特征值较小， 故构成这一特征向量的变量间有近似的线性关系。

在统计中用方差比例来说明各个自变量在构成这个特征向量中的贡献。一般建议， 在大的条件指数中由方差比例超过0. 5 的自变量构成的变量子集就认为是相关变量集。

5.回归分析方法

§3.2 回归分析方法 回归分析方法，是研究要素之间具体的数量关系的一种强有力的工具，能够建立反映地理要素之间具体的数量关系的数学模型，即回归模型。

1. 一元线性回归模型 1） 一元线性回归模型的基本结构形式 假设有两个地理要素（变量）x和y,x为自变量，y为因变量。则一元线性回归模型的基本结构形式：a和b为待定参数；α=1,2，…，n为各组观测数据的下标； εa为随机变量。

如果记a^和b^ 分别为参数a与b的拟合值，则得到一元线性回归模型 ÿ 是y 的估计值，亦称回归值。回归直线——代表x与y之间相关关系的拟合直线 2） 参数a、b的最小二ÿ乘估计 参数a与b的拟合值：， 建立一元线性回归模型的过程，就是用变量 和 的实际观测数据确定参数a和b的最小二乘估计值α^和β^ 的过程。

3） 一元线性回归模型的显著性检验 线性回归方程的显著性检验是借助于F检验来完成的。 检验统计量F： 误差平方和： 回归平方和： F≈F(1,n-2)。

在显著水平a下，若 ，则认为回归方程效果在此水平下显著；当 时，则认为方程效果不明显。[举例说明] 例1：在表3.1.1中，将国内生产总值（x1）看作因变量y，将农业总产值（x2）看作自变量x，试建立它们之间的一元线性回归模型并对其进行显著性检验。

解： （1） 回归模型 将y和x的样本数据代入参数a与b的拟合公式，计算得：故，国内生产总值与农业总产值之间的回归方程为（2） 显著性检验 在置信水平α=0.01下查F分布表得：F0.01(1,46)=7.22。由于F=4951.098 >> F0.01(1,46)=7.22，所以回归方程（3.2.7）式在置信水平a=0.01下是显著的。

2. 多元线性回归模型 在多要素的地理系统中，多个（多于两个）要素之间也存在着相关影响、相互关联的情况。因此，多元地理回归模型更带有普遍性的意义。

1） 多元线性回归模型的建立 （1） 多元线性回归模型的结构形式 假设某一因变量y受k 个自变量 的影响，其n组观测值为 。则多元线性回归模型的结构形式：为待定参数， 为随机变量。

如果 分别为 的拟合值，则回归方程为 b0为常数， 称为偏回归系数。 偏回归系数 ——当其它自变量都固定时，自变量 每变化一个单位而使因变量xi平均改变的数值。

（2） 求解偏回归系数， 2） 多元线性回归模型的显著性检验 用F检验法。 F统计量：当统计量F计算出来之后，就可以查F分布表对模型进行显著性检验。

[举例说明] 例2：某地区各城市的公共交通营运总额（y）与城市人口总数（x1 ）以及工农业总产值（x2）的年平均统计数据如表3.2.1（点击展开显示该表）所示。试建立y与x1及x2之间的线性回归模型并对其进行显著性检验。

表3.2.1 某地区城市公共交通营运额、人口数及工农业总产值的年平均数据 城市序号 公共交通营运额y/103人公里 人口数x1/103人 工农业总产值x2/107元 1 6825.99 1298.00 437.26 2 512.00 119.80 1286.48 。 。

。 。

14 192.00 12.47 1072.27 注：本表数据详见书本P54。 解： （1） 计算线性回归模型 由表3.2.1中的数据，有 计算可得：故y与x1 及y2之间的线性回归方程（2） 显著性检验 故：在置信水平a=0.01下查F分布表知：F0.01(2,11)=7.21。

由于F=38.722> F0.01(2,11)=7.21，所以在置信水平a=0.01下，回归方程式是显著的。3. 非线性回归模型的建立方法 1） 非线性关系的线性化 （1） 非线性关系模型的线性化 对于要素之间的非线性关系通过变量替换就可以将原来的非线性关系转化为新变量下的线性关系。

[几种非线性关系模型的线性化] ① 于指数曲线 ，令 ， ，将其转化为直线形式： ，其中， ； ② 对于对数曲线 ，令 ， ，将其转化为直线形式： ； ③ 对于幂函数曲线 ，令 ， ，将其转化为直线形式： ，其中， ④ 对于双曲线 ，令 ，将其转化为直线形式：； ⑤ 对于S型曲线 ，将其转化为直线形式：； ⑥ 对于幂函数乘积：令 将其转化为直线形式：其中， ； ⑦ 对于对数函数和：令 ，将其化为线性形式：（2） 建立非线性回归模型的一般方法 ① 通过适当的变量替换将非线性关系线性化； ② 用线性回归分析方法建立新变量下的线性回归模型： ③ 通过新变量之间的线性相关关系反映原来变量之间的非线性相关关系。 3） 非线性回归模型建立的实例 非线性回归模型建立的实例 景观是地理学的重要研究内容之一。

有关研究表明（Li,2000；徐建华等，2001），任何一种景观类型的斑块，其面积（Area）与周长（Perimeter）之间的数量关系可以用双对数曲线来描述，即 例3：表3.2.2给出了某地区林地景观斑块面积（Area）与周长（Perimeter）的数据。试建立林地景观斑块面积A与周长P之间的双对数相关关系模型。

表3.2.2某地区各个林地景观斑块面积（m2）与周长（m） 序号 面积A 周长P 序号 面积A 周长P 1 10447.370 625.392 42 232844.300 4282.043 2 15974.730 612.286 43 4054.660 289.307 。 。

。 。

。 。

41 1608.625 225.842 82 564370.800 12212.410 注：本表数据详见书本57和58页。 解：因为林地景观斑块面积（A）与周长（P）之间的数量关系是双对数曲线形式，即 所以对表3.2.2中的原始数据进行对数变换，变换后得到的各新变量对应的观测数据如表3.2.3所示。

6.计量经济学,回归方法fen xi

1、稳健回归其主要思路是将对异常值十分敏感的经典最小二乘回归中的目标函数进行修改。

经典最小二乘回归以使误差平方和达到最小为其目标函数。因为方差为一不稳健统计量，故最小二乘回归是一种不稳健的方法。

为减少异常点的作用，对不同的点施加不同的权重，残差小的点权重大，残差大的店权重小。2、变系数回归 地理位置加权3、偏最小二乘回归长期以来，模型式的方法和认识性的方法之间的界限分得十分清楚。

而偏最小二乘法则把它们有机的结合起来了，在一个算法下，可以同时实现回归建模（多元线性回归）、数据结构简化（主成分分析）以及两组变量之间的相关性分析（典型相关分析）。偏最小二乘法在统计应用中的重要性体现在以下几个方面：偏最小二乘法是一种多因变量对多自变量的回归建模方法。

偏最小二乘法可以较好的解决许多以往用普通多元回归无法解决的问题。偏最小二乘法之所以被称为第二代回归方法，还由于它可以实现多种数据分析方法的综合应用。

能够消除自变量选取时可能存在的多重共线性问题。普通最小二乘回归方法在自变量间存在严重的多重共线性时会失效。

自变量的样本数与自变量个数相比过少时仍可进行预测。4、支持向量回归 能较好地解决小样本、非线性、高维数和局部极小点等实际问题。

传统的化学计量学算法处理回归建模问题在拟合训练样本时，要求“残差平方和”最小，这样将有限样本数据中的误差也拟合进了数学模型，易产生“过拟合”问题，针对传统方法这一不足之处，SVR采用“ε不敏感函数”来解决“过拟合”问题，即f(x)用拟合目标值yk时，取：f(x) =∑SVs（αi-α*i）K(xi,x) 上式中αi和α*i为支持向量对应的拉格朗日待定系数，K(xi,x)是采用的核函数[18],x为未知样本的特征矢量，xi为支持向量（拟合函数周围的ε“管壁”上的特征矢量），SVs为支持向量的数目.目标值yk拟合在yk-∑SVs（αi-α*i）K(xi,xk)≤ε时，即认为进一步拟合是无意义的。5、核回归 核函数回归的最初始想法是用非参数方法来估计离散观测情况下的概率密度函数（pdf）。

为了避免高维空间中的内积运算 由Mercer条件，存在映射函数a和核函数K（？，？)，使得：=K(xi ,x)采用不同的函数作为SVM的核函数K (x i,x)，可以实现多种从输入空间到特征空间的非线性映射形式6、岭回归 岭回归分析是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的耐受性远远强于最小二乘法。7、半参数回归 模型既含有参数分量又含有非参数分量，其参数部分用来解释函数关系已知的部分，它是观测值中的主要成分，而其非参数部分则描述函数关系未知，无法表达为待定参数的函数部分。

8、自回归例1.Yt = α+β0Xt +β1Xt-1 +……+βsXt-s + ut，例2.Yt = f (Yt-1, Yt-2， … ， X2t, X3t， … ) ，滞后的因变量（内生变量）作为解释变量出现在方程的右端。这种包含了内生变量滞后项的模型称为自回归模型。

9、正交回归 因素水平值在区间[Zj1, Zj2]内变化，经编码之后，编码值xi在区间[-1,+1]间变化，将响应值y原来对Z1, Z2……Zm的回归问题，转化为y对x1,x2……xm的回归问题。它的主要优点是可以把实验或计算的安排、数据的处理和回归方程的精度统一起来加以考虑，根据实验目的和数据分析来选择实验或计算点，不仅使得在每个实验或计算点上获得的数据含有最大的信息，从而减少实验或计算次数，而且使数据的统计分析具有一些较好的性质，以较少的实验或计算建立精度较高的回归方程。

10、逐步回归 实际问题中影响因变量的因素可能很多，我们希望从中挑选出影响显著的自变量来建立回归模型，这就涉及到变量选择的问题，逐步回归是一种从众多变量中有效地选择重要变量的方法。基本思路为，先确定一初始子集，然后每次从子集外影响显著的变量中引入一个对y 影响最大的，再对原来子集中的变量进行检验，从变得不显著的变量中剔除一个影响最小的，直到不能引入和剔除为止。

11、主成分回归 在统计学中，主成分分析是一种简化数据集的技术。它是一个线性变换。

这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标（称为第一主成分）上，第二大方差在第二个坐标（第二主成分）上，依次类推。 首先对X阵进行主成份分析，T阵的维数可以与X阵相同，如果使用整个T阵参加回归，这样得到的结果与多元线性回归没有多大的差别。

因为主成分（新变量）是原变量的线性组合。前面的k个主成份包含了X矩阵的绝大部分有用信息，而后面的主成份则往往与噪声和干扰因素有关。

因此参与回归的是少数主成分组成的矩阵。在维数上远小于X。

主成分回归通过对参与回归的主成份的合理选择，可以去掉噪音。主成份间相互正交，解决了多元线性回归中的共线性问题。

主成分回归能够充分利用数据信息，有效地提高模型的抗干扰能力。